Çemberin Temel Elemanları ve Kiriş 11. Sınıf
Çemberde Teğet, Kiriş, Çap, Yay ve Kesen
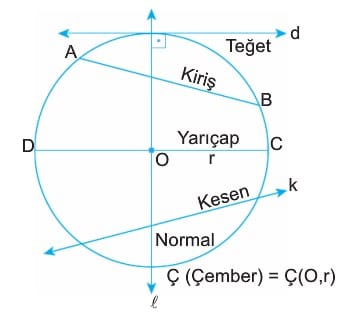
Düzlemde sabit bir noktaya (merkez) eşit uzaklıkta (yarıçap) bulunan noktalar kümesine çember denir.
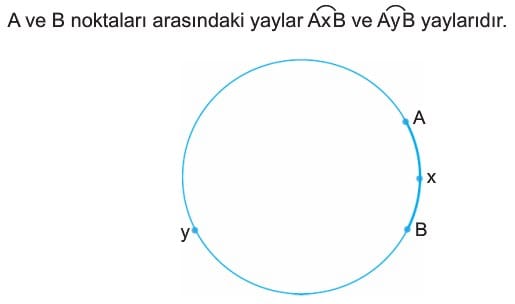
Yay
Bir çember üzerindeki farklı iki nokta arasında kalan çembere ait noktalar kümesine çember yayı denir.
Teğet
Bir çember ile tek bir ortak noktası olan doğruya çemberin bir teğet doğrusu denir.
Kesen
Çemberi farklı iki noktada kesen doğruya çemberin keseni denir.
Kiriş
Bir çemberin farklı iki noktasını birleştiren doğru parçasına çemberin kirişi denir.
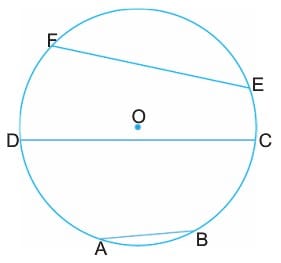
[AB], [DC], [EF] doğru parçaları O merkezli çemberin kirişleridir.
Çap
Merkezden geçen kirişe çap denir.
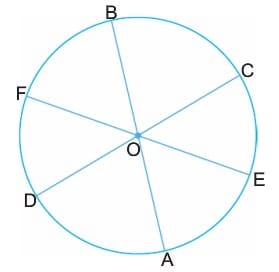
[AB], [CD], [EF] doğru parçaları O merkezli çemberin çap doğrusudur. Bu doğruların uzunlukları çemberin çap uzunluğu olur.
Bir Düzlemde Bir Çember ile Bir Doğrunun Birbirlerine Göre Durumları
Bir çember ile bir doğru 3 farklı konumda olabilir.
1. Doğru çemberi kesmez
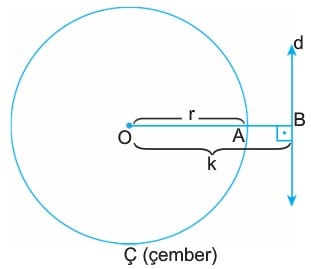
O noktasından doğruya olan uzaklık (dik) yarıçaptan büyük ise doğru ile çember kesişmez.
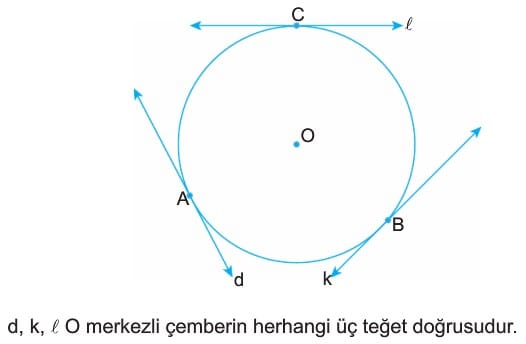
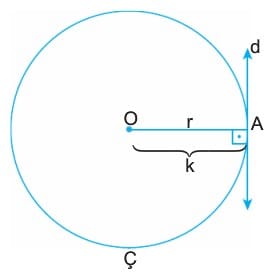
2. Doğru çembere teğet olur.
Çemberin merkezinin d doğrusuna olan uzaklığı yarıçapa eşit olduğunda “çember doğruya teğettir” denir. Çember ile doğrunun bu durumda tek bir ortak noktası (A) olur.
BİLGİ: Çember üzerindeki bir noktadan çembere yalnız bir teğet doğrusu çizilir.
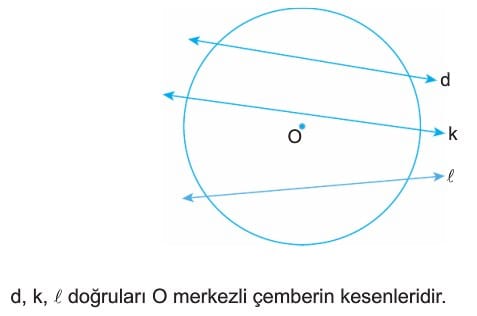
3. Çember ile doğru farklı iki noktada kesişir.
Çember merkezinden doğruya olan uzaklık çemberin yarıçapından küçük ise doğru çemberi iki farklı noktada keser.
Çemberde Kirişin Özellikleri
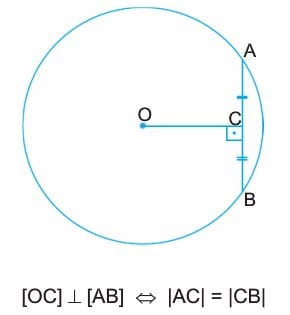
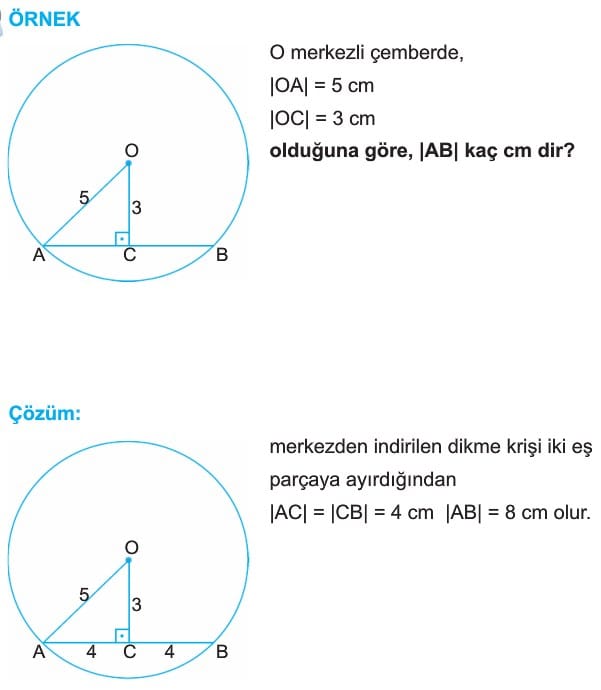
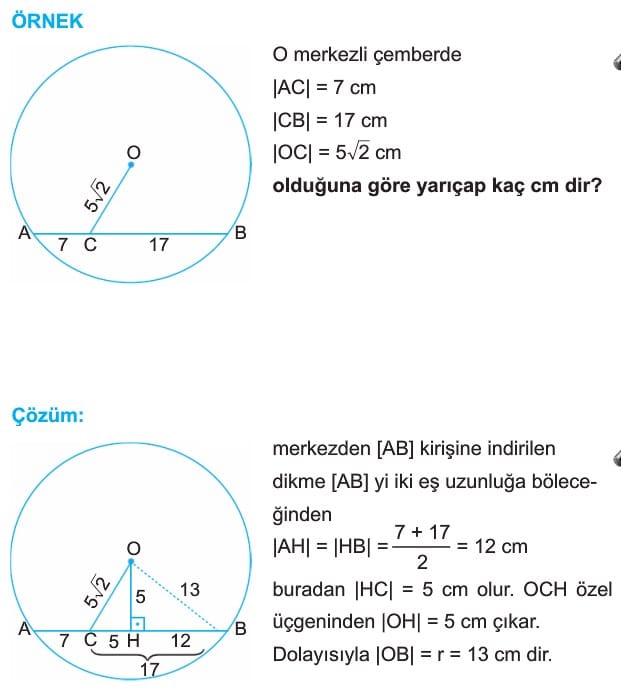
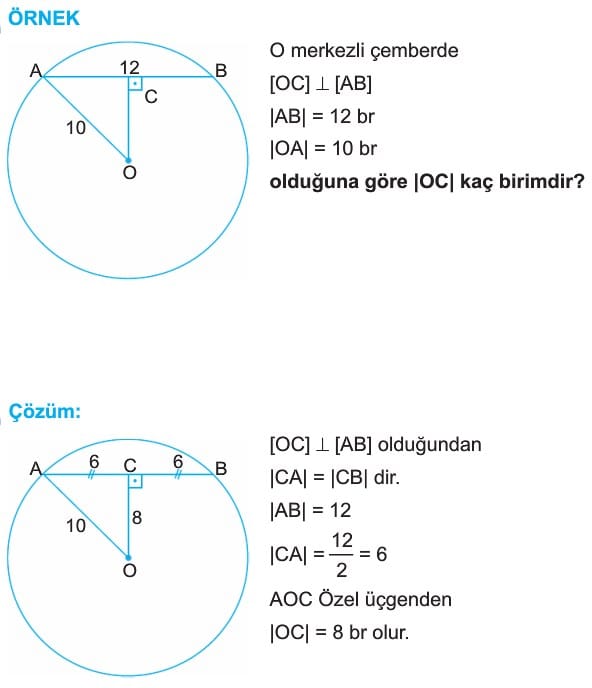
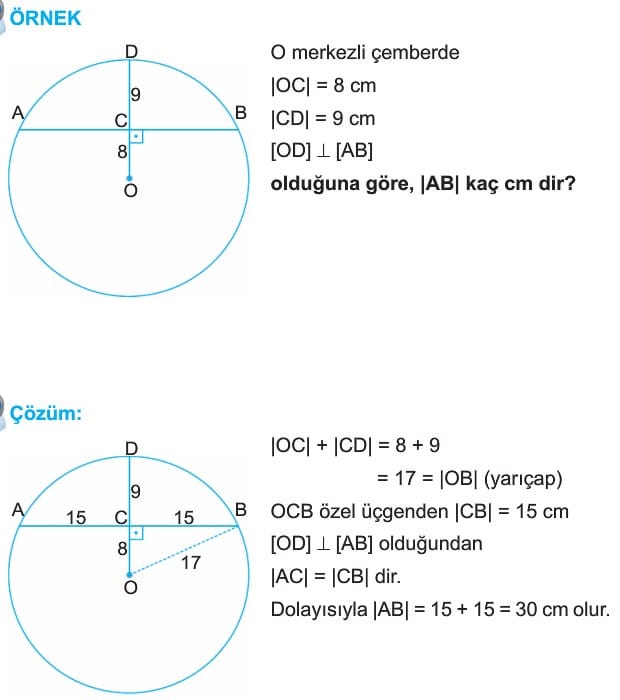
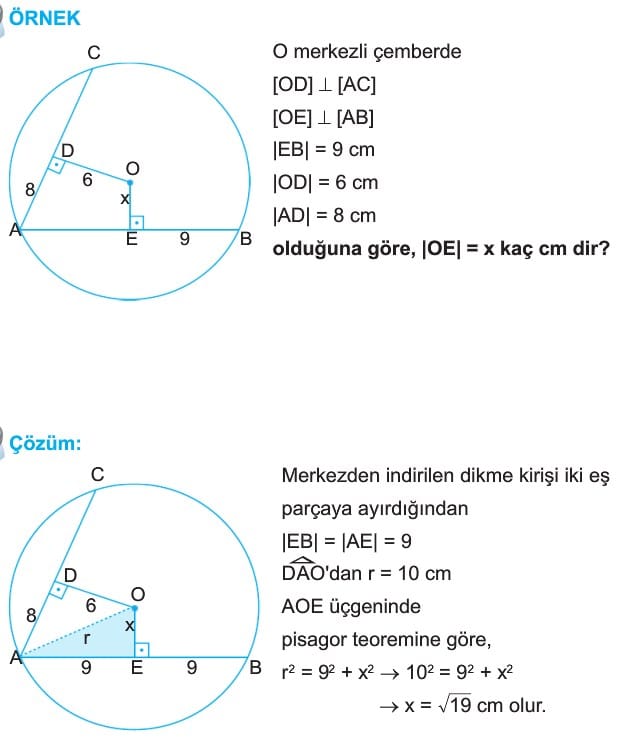
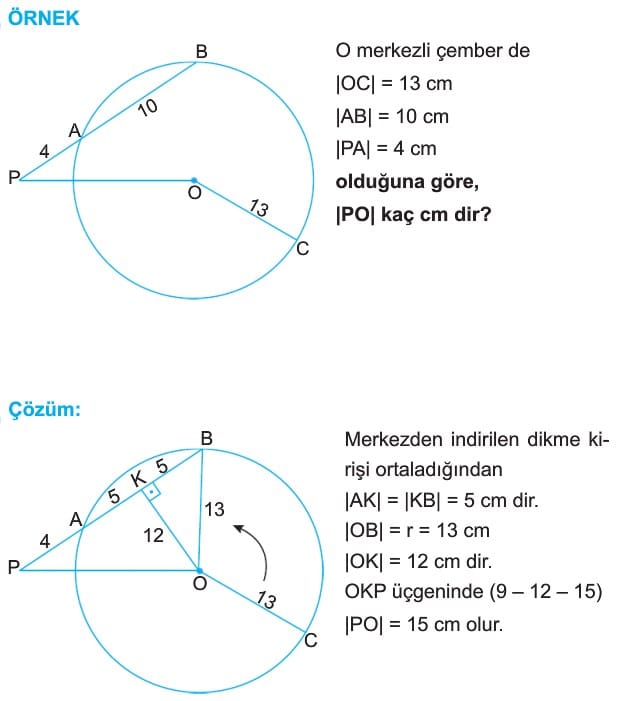
1. Bir çemberin merkezinden herhangi bir kirişe çizilen dik doğru kirişi iki eş parçaya ayırır.
Bilgi: Çemberde kirişin orta dikmesi çemberin merkezinden geçer.
bu durumda AOB üçgeni ikizkenar üçgen olur.
Bilgi: Çemberde en büyük kiriş çaptır.
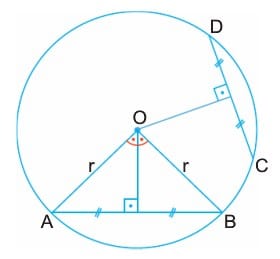
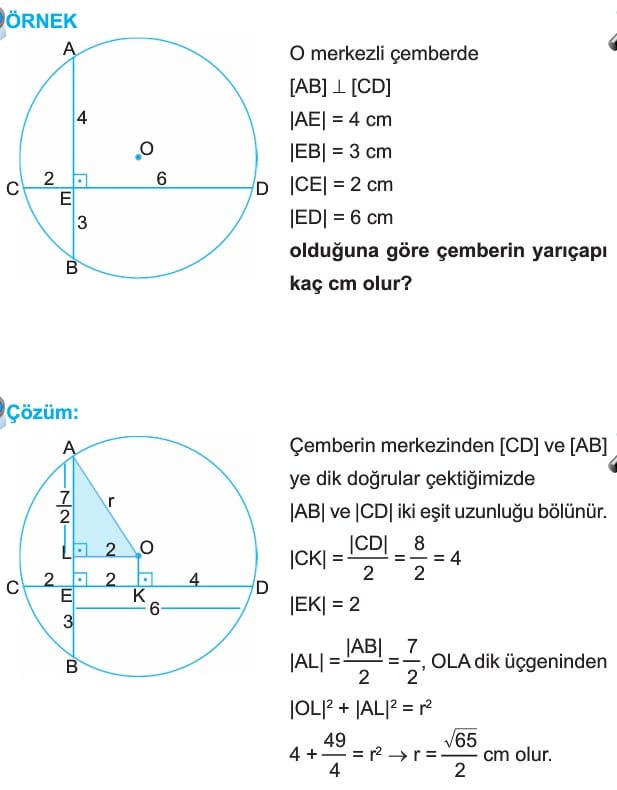
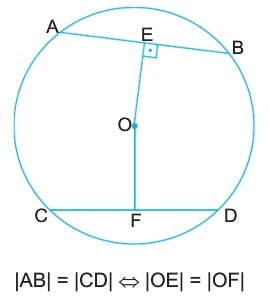
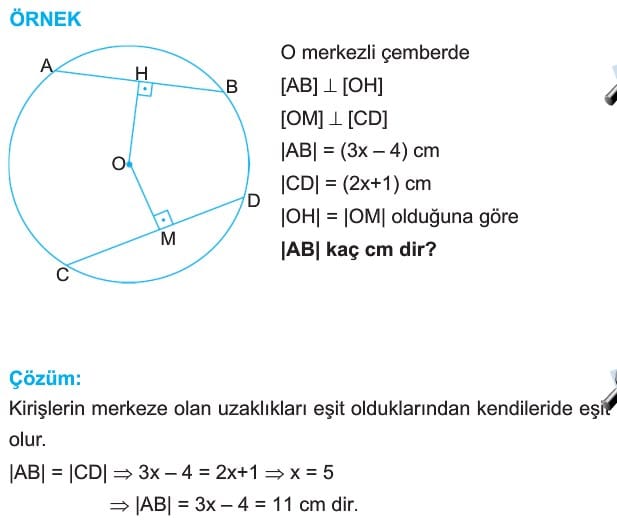
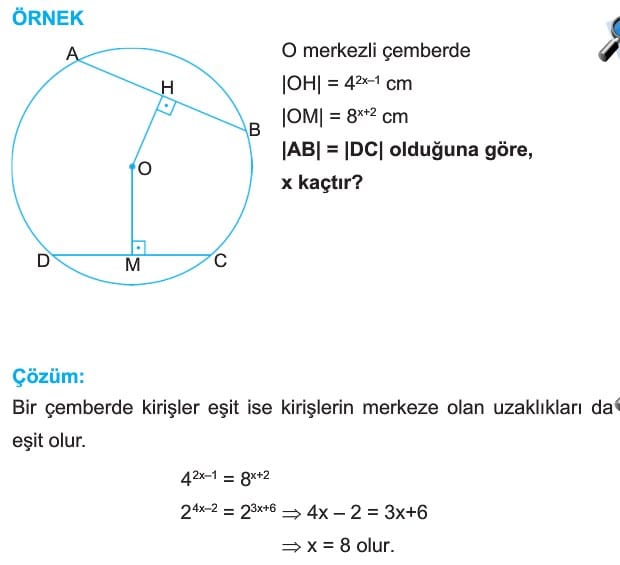
2. Bir çemberde eşit uzunluktaki kirişlerin çemberin merkezine olan uzaklıkları eşittir.
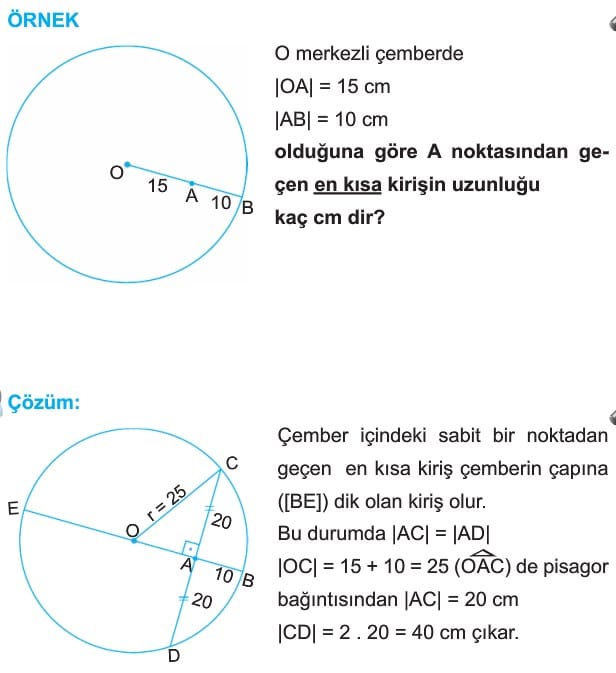
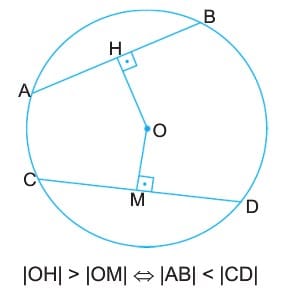
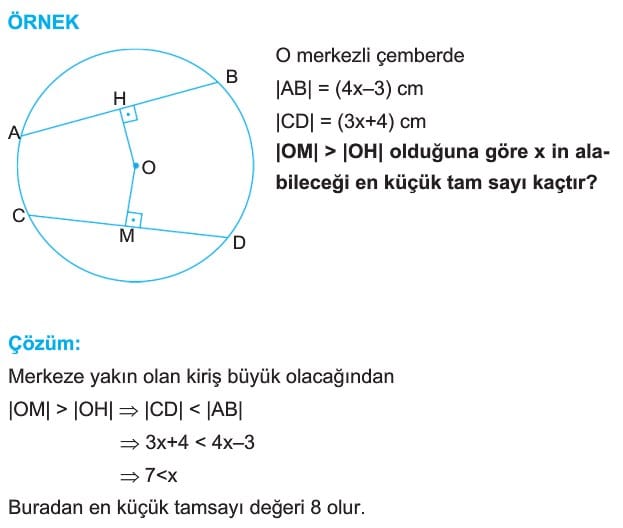
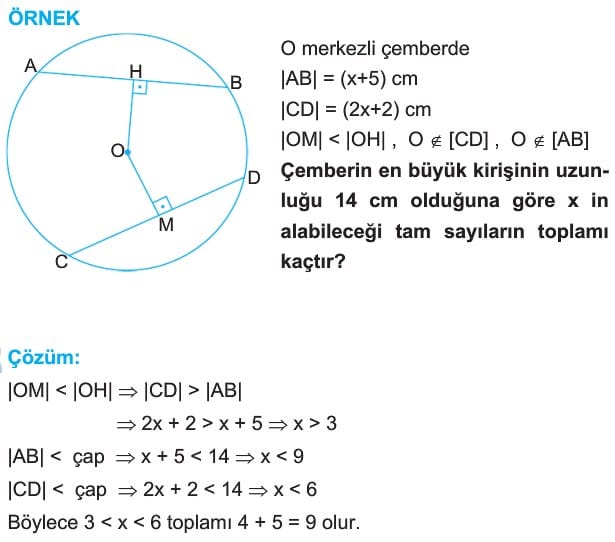
3. Bir çemberde kiriş merkeze yaklaştıkça uzunluğu artar.
Bilgi: Çemberde en büyük kiriş çaptır.
Çözümlü Örnek Test Soruları
Soru 1
Bir çemberin çapı 16 cm ise, çemberin yarıçapı kaç cm’dir?
A) 8
B) 10
C) 12
D) 14
E) 16
Çözüm: Çemberin çapı, yarıçapın iki katıdır. Bu durumda yarıçap 16 ÷ 2 = 8 cm’dir.
Cevap: A
Soru 2
Yarıçapı 10 cm olan bir çemberde, çemberin çevresinin uzunluğu yaklaşık kaç cm’dir? (π ≈ 3,14 alın)
A) 31,4
B) 50
C) 62,8
D) 75
E) 100
Çözüm: Çemberin çevresi formülü: 2πr’dir. Çevre = 2 × 3,14 × 10 = 62,8 cm olur.
Cevap: C
Soru 3
Bir çemberde, AB kirişi çemberin merkezine dik olarak 12 cm uzunluğunda bir kiriştir. Çemberin yarıçapı kaç cm’dir?
A) 6
B) 8
C) 10
D) 15
E) 18
Çözüm: Merkeze dik olan kirişin ortası, yarıçap ile merkez arasında bir dik üçgen oluşturur. Hipotenüs (yarıçap) ve dik kenarlar (kirişin yarısı ve merkeze olan uzaklık) dik üçgende Pisagor Teoremi ile bulunur. Kirişin yarısı 6 cm olduğundan, rr = 66 + (merkez uzaklığı)* (merkez uzaklığı) şeklinde hesaplanır.
Cevap: C
Soru 4
Yarıçapı 8 cm olan bir çemberde, merkezden 6 cm uzaklıkta bir kirişin uzunluğu kaç cm’dir?
A) 10
B) 12
C) 14
D) 16
E) 18
Çözüm: Merkeze 6 cm uzaklıktaki bir kiriş için Pisagor bağıntısından yararlanılır. r*r = (kirişin yarısı) * (kirişin yarısı) + (merkeze olan uzaklık) * (merkeze olan uzaklık) olduğundan, hesaplama yapılır.
Cevap: B
Soru 5
Merkezi O olan çemberde, OA = OB = 10 cm ve AB = 12 cm. Bu durumda A ve B noktaları arasındaki yay kaç derecedir?
A) 60°
B) 90°
C) 120°
D) 150°
E) 180°
Çözüm: OA ve OB yarıçap olduğu için AOB üçgeni ikizkenardır. Kiriş uzunluğu ile yay ölçüsü arasındaki ilişki ile çözüm yapılır.
Cevap: B
Soru 6
Merkezden geçen bir çemberde iki kirişin uzunlukları 6 cm ve 8 cm’dir. Bu kirişlerin çember merkezine uzaklıkları arasındaki fark kaç cm’dir?
A) 1
B) 2
C) 3
D) 4
E) 5
Çözüm: Merkezden uzaklık ile kiriş uzunluğu arasındaki bağıntı ve Pisagor teoremi kullanılarak merkezden uzaklık farkı bulunur.
Cevap: C
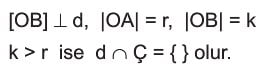
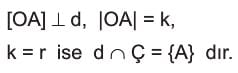
teşekkürlerr