Çemberde Teğet 11. Sınıf

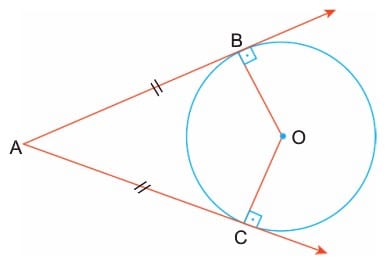
Kategoriler: 11. sınıf Matematik, Matematik

1. Bir çembere dışındaki bir noktadan çizilen teğet uzunlukları eşittir.

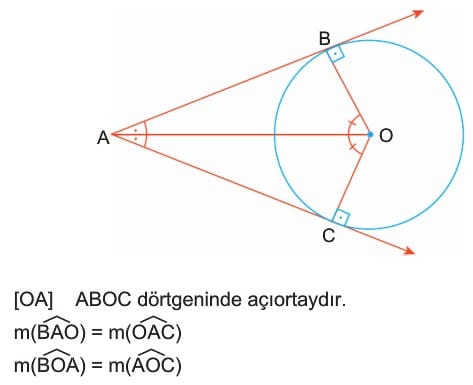
Bilgi: Bir çembere dışındaki bir noktadan çizilen teğetlerin arasında kalan ve çemberi gören açının açıortayı çemberin merkezinden geçer.

2. İç Teğet Çember

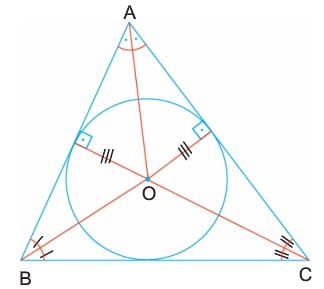
ABC üçgeninde açıortayların kesim noktası iç teğet çemberin merkezi olur.

Bilgi: Herhangi bir Üçgende iç açıortaylar tek bir noktadan kesişir.

3. Dış Teğet Çember

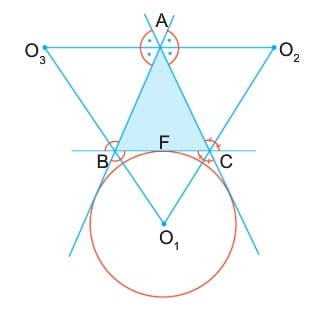
İki dış açının açıortaylarının kesim noktası üçgenin dış teğet çemberinin merkezidir. Şekilde O1, O2, O3 noktaları ABC Üçgeninin dış teğet çemberlerinin merkezleridir.

Bilgi: Bir Üçgende iki dış açıortayla bunlara komşu olmayan bir iç açıortay bir noktada kesişir.

Çemberde Teğet Soruları ve Çözümleri

] }

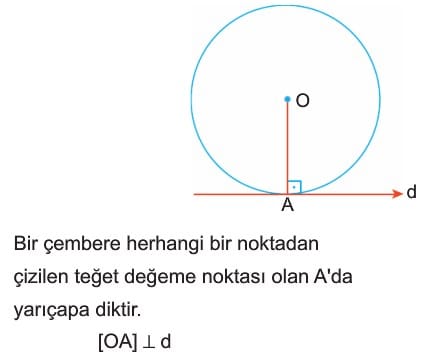
Bir çembere herhangi bir noktadan çizilen teğet değme noktası olan A'da yarıçapa diktir.
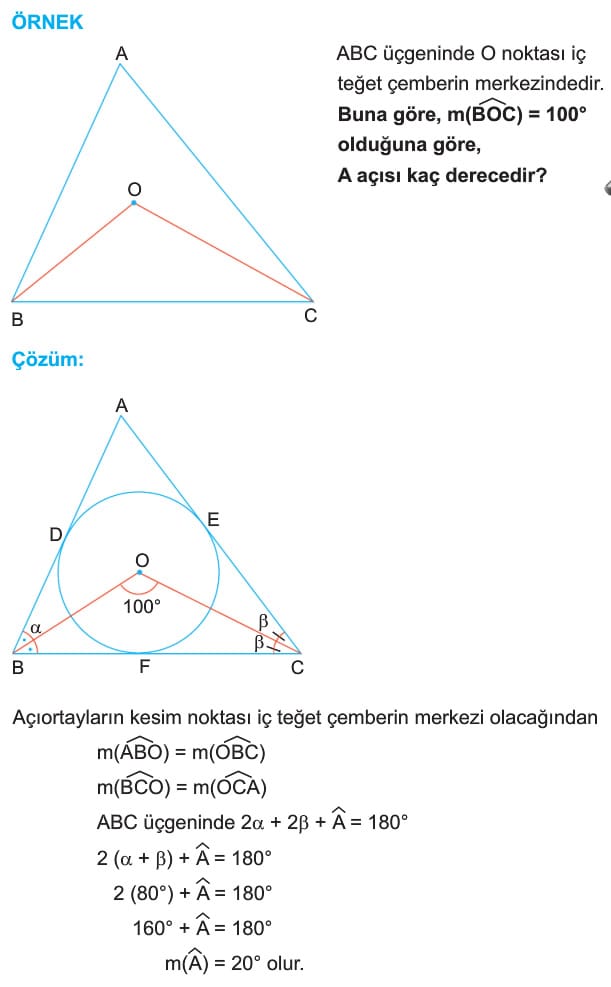
Soru: ABC üçgeninde O noktası iç teğet çemberin merkezindedir. Buna göre, m(BAC) = 100° olduğuna göre, A açısı kaç derecedir?

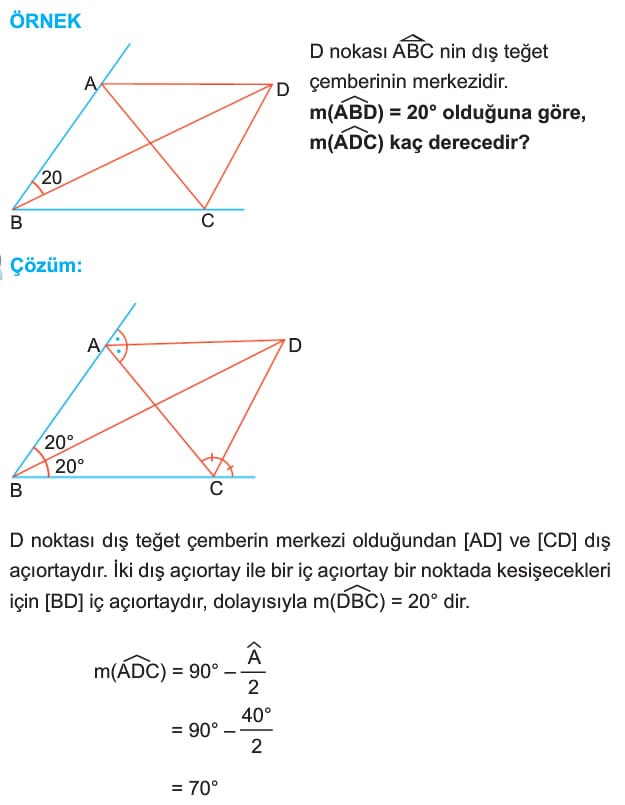
Örnek: D nokası ABC nin dış teğet çemberinin merkezidir.
m(ABD) = 20° olduğuna göre,
m(ADC) kaç derecedir?
Çözüm: D noktası dış teğet çemberin merkezi olduğundan [AD] ve [CD] dış açıortaydır. İki dış açıortay ile bir iç açıortay bir noktada kesişecekleri için [BD] iç açıortaydır, dolayısıyla m(DBC) = 20° dir.

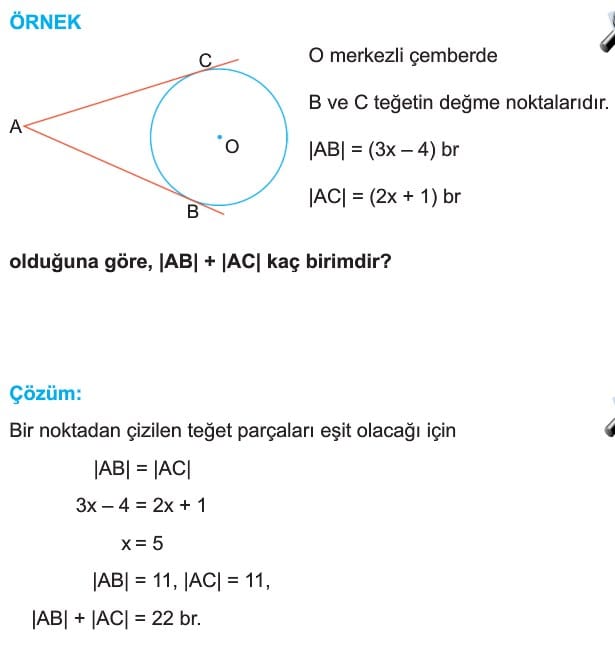
Örnek: O merkezli çemberde B ve C teğetin değme noktalarıdır.
|AB| = (3x - 4) birim
|AC| = (2x + 1) birim
olduğuna göre, |AB| + |AC| kaç birimdir?
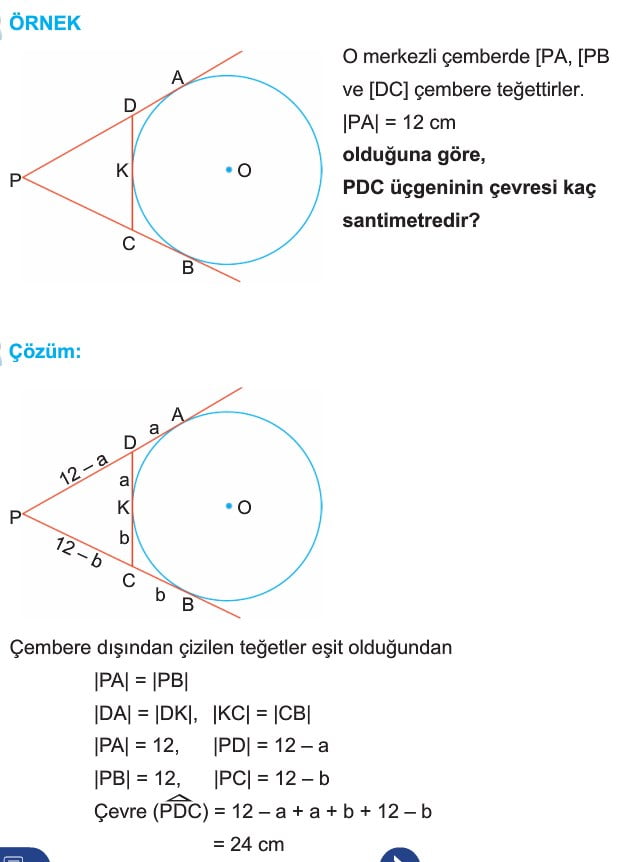
Çözüm: Bir noktadan çizilen teğet parçaları eşit olacağı için
|AB| = |AC|
3x - 4 = 2x + 1
x = 5
|AB|=11, |AC|=11,
|AB| + |AC| = 22 birim.

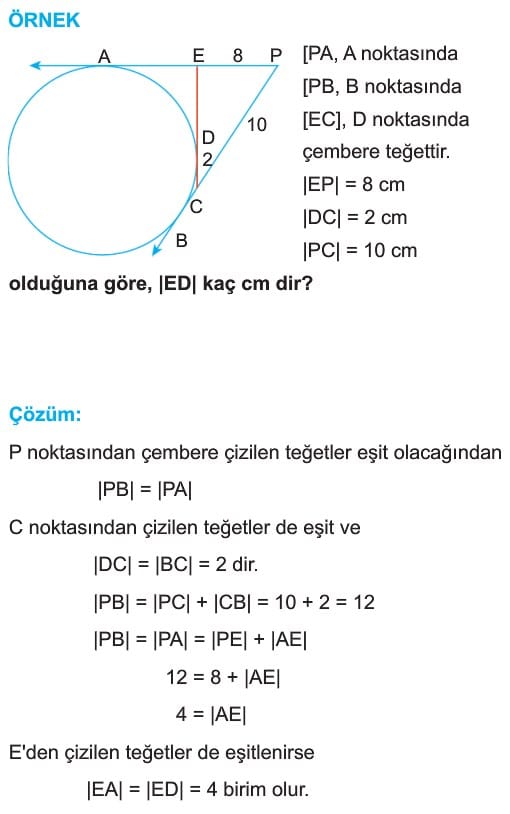
Örnek: [PA, A noktasında
[PB, B noktasında
[EC], D noktasında çembere teğettir.
|EP| = 8 cm
|DC| = 2 cm
|PC| = 10 cm
olduğuna göre, |ED| kaç cm dir?
Çözüm: P noktasından çembere çizilen teğetler eşit olacağından
|PB| = |PA| C noktasından çizilen teğetler de eşit ve
|DC| = |BC| = 2 dir.
|PB| = |PC| + |CB| = 10 + 2 = 12
|PB| = |PA| = |PE| + |AE|
12 = s + |AE|
4 = |AE|
E'den çizilen teğetler de eşitlenirse |EA| = |ED| = 4 birim olur.

Aşağıdaki ifadelerden doğru olanların başına "D" yanlış olanların başına "Y" harfi koyunuz.
1. Bir çembere dışındaki bir noktadan en fazla 2 tane teğet doğrusu çizilebilir.
2. Teğet doğrusu çembere bir noktada değer.
3. Bir çembere dışındaki bir noktadan çizilen teğet parçalarının uzunlukları eşittir.
4. Çemberin dışındaki bir noktadan, çembere teğet doğrusu çizilebilir.
5. Aynı merkezli çemberlerin yarıçap uzunlukları eşit ise çemberler çakışıktır.
6. Farklı iki çember en fazla iki noktada kesişir.
7. Çemberin içindeki bir noktadan çembere bir teğet doğrusu çizilir.
8. Çemberin içine çizilen ve köşeleri çember üzerinde bulunan dörtgene kirişler dörtgeni denir.
9. Bir dörtgenin içine çizilen çember dörtgenin tüm kenarlarına teğet ise dörtgene teğetler dörtgeni denir.
10. İki çember iki şekilde birbirine teğet olurlar.
11. Bir ışın çembere teğet olamaz.

Liselere Giriş Sınavı (LGS)
5 Haziran 2022 Pazar
Temel Yeterlilik Sınavı (TYT)
18 Haziran 2022 Cumartesi
Alan Yeterlilik Sınavı (AYT)
19 Haziran 2022 Pazar