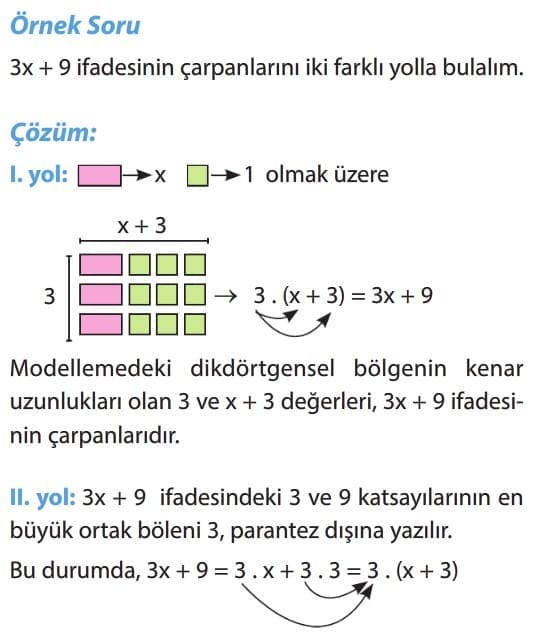
Cebirsel İfadeleri Çarpanlara Ayırma 8. Sınıf
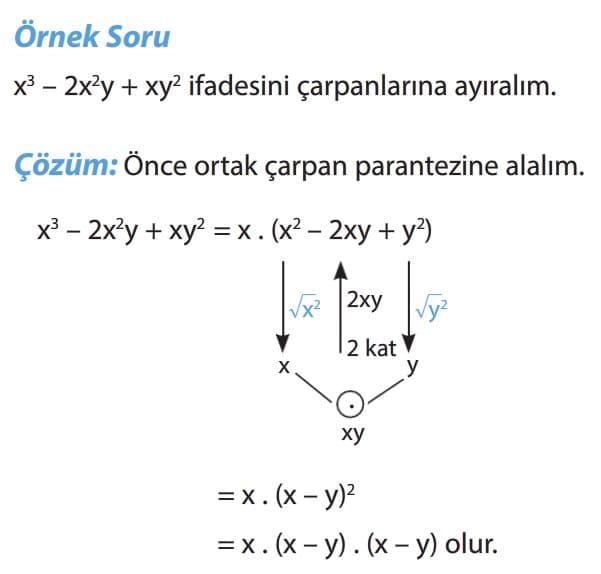
ORTAK ÇARPAN PARANTEZİNE ALARAK ÇARPANLARA AYIRMA
Her terimde katsayıların en büyük ortak böleni (EBOB) veya her terimdeki aynı (ortak) çarpan ifadelerinin parantez dışına alınmasına ortak çarpan parantezine alarak çarpanlara ayırma denir.
Dikkat: Bir cebirsel ifadeyi ortak çarpan parantezine alırken cebirsel ifadedeki katsayıların EBOB’u ile tüm terimlerde ortak olan en küçük üsse sahip değişkeni parantezin dışına yazmak işlemde kolaylık sağlar.
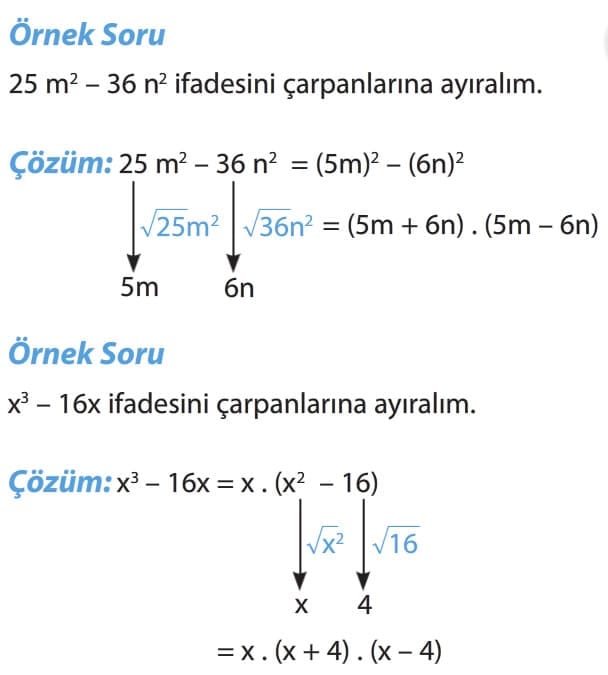
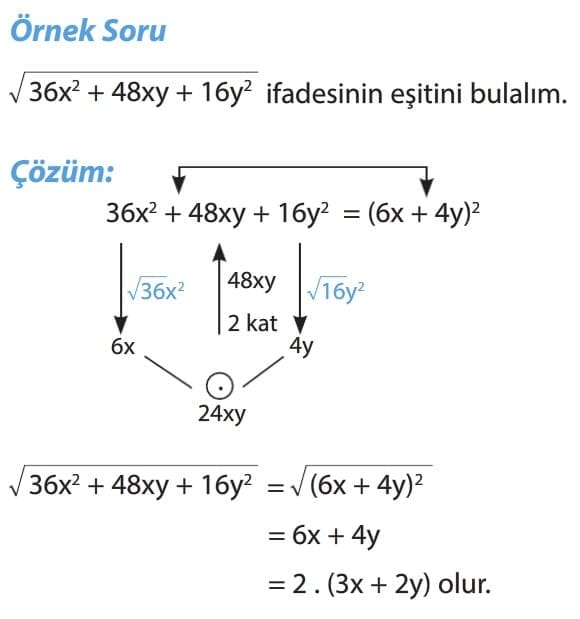
İKİ KARE FARKI ŞEKLİNDE VERİLEN BİR İFADEYİ ÇARPANLARA AYIRMA
Önemli Bilgi: İki kare farkı şeklinde verilen bir ifadeyi çarpanlarına ayırmak için önce verilen terimlerin karekökleri alınır. İfade bulunan kareköklerin toplamı ile farkının çarpımı şeklinde yazılır.
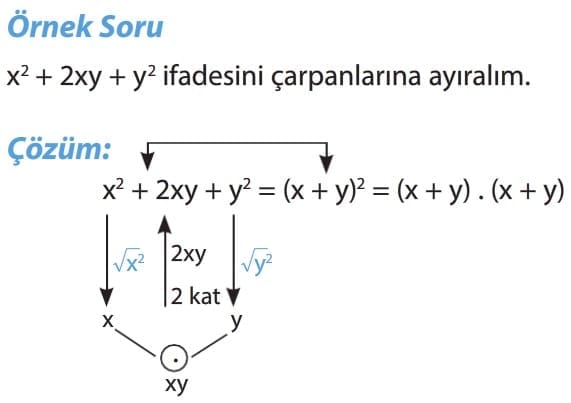
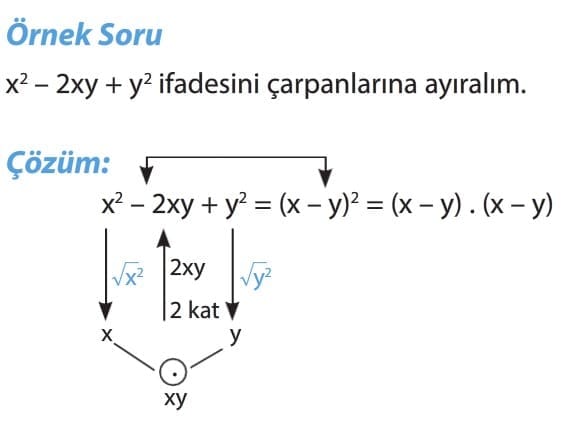
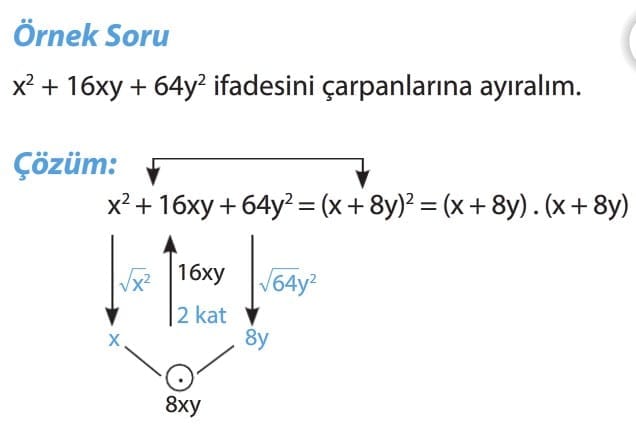
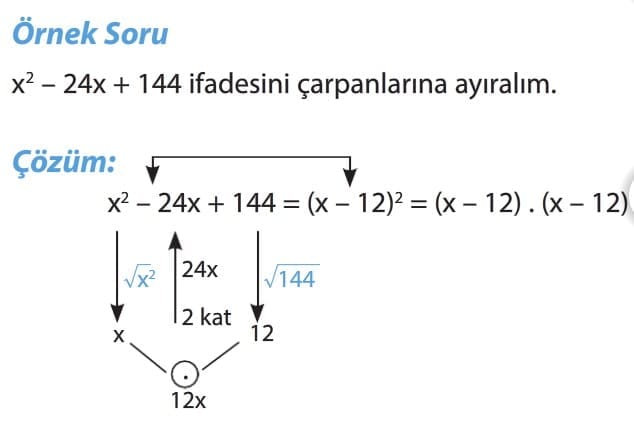
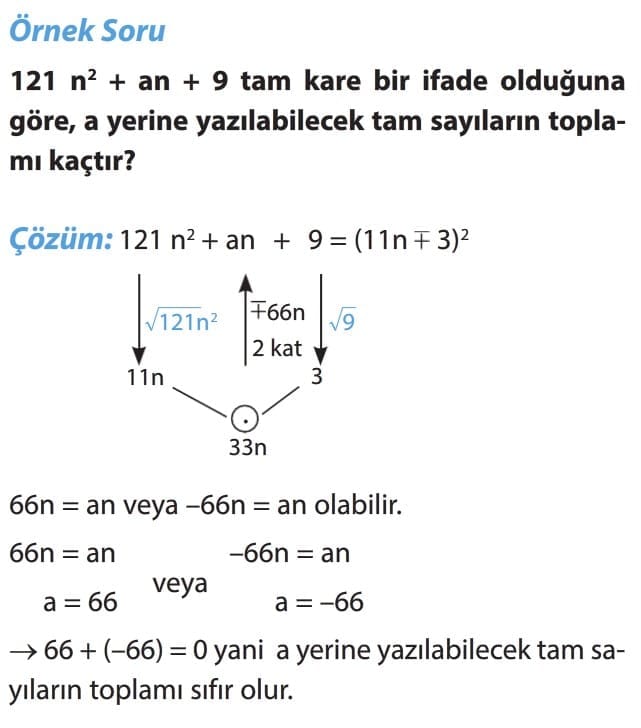
TAM KARE ŞEKLİNDE VERİLEN BİR İFADEYİ ÇARPANLARA AYIRMA
Önemli Bilgi: Tam kare şeklinde verilen bir ifadeyi çarpanlarına ayırırken birinci terim ile üçüncü terimin karekökü alınır. Karekök değerlerinin çarpımının iki katı ortanca terime eşit ise birinci terimin karekökü ile üçüncü terimin karekökü, ortanca terimin işaretine bakılarak toplam ya da farkların karesi şeklinde yazılır.
Cebirsel İfadeleri Çarpanlara Ayırma 8. Sınıf konu anlatımı Çözümlü Sorular Lgs
Örnek Soru: 5x2 + 6x ifadesini çarpanlarına ayıralım.
Çözüm: 5x2 + 6x ifadesinde katsayıların en büyük ortak böleni 1'dir ve değişkenlerdeki en küçük üsse sahip olan x'tir.
5x2 + 6x = x . (5x + 6) elde edilir.
Örnek Soru: 9x3 - 27x2 + 36x ifadesinin çarpanlarını bulalım.
Çözüm: 9x3 - 27x2 + 36x ifadesindeki 9, 27 ve 36 sayılarının en büyük ortak böleni 9'dur. x3, x2 ve x ifadelerindeki en küçük üsse sahip olan x'tir. 9 ve x parantez dışına yazılırsa 9x3 - 27x2 + 36x = 9x. (x2 - 3x + 4) elde edilir. 9x3 - 27x2 + 36x ifadesinin çarpanlarından biri 9x diğeri (x2 - 3x +4) olur.
Örnek Soru: -18x4 - 20x2 ifadesini çarpanlarına ayıralım.
Çözüm: -1 8x4- 20x2 ifadesinde en büyük ortak bölen katsayılar için -2, değişkenler için x2dir. -18x4- 20x2 = -2x2 . (9x2 + 10) elde edilir. Buna göre, -18x4 - 20x2 ifadesinin çarpanlarından biri -2x2 diğeri (9x2 + 10) olur.
Soru: Mehtap; bir kenarının uzunluğu a cm olan kare biçimindeki bir kâğıdı, kesikli çizgiler boyunca önce yatay sonra dikey olarak şekildeki gibi 2b cm uzunluğunda katlayıp tekrar geri açıyor. Buna göre, en son durumda kat izlerinin oluşturduğu dörtgensel bölgelerden birinin alanını santimetrekare cinsinden gösteren cebirsel ifade aşağıdakilerden hangisi olamaz?
A) 2ab - 4b2 B) az - 4ab + 4b2 c) a2 - 4b2 D) 4b2