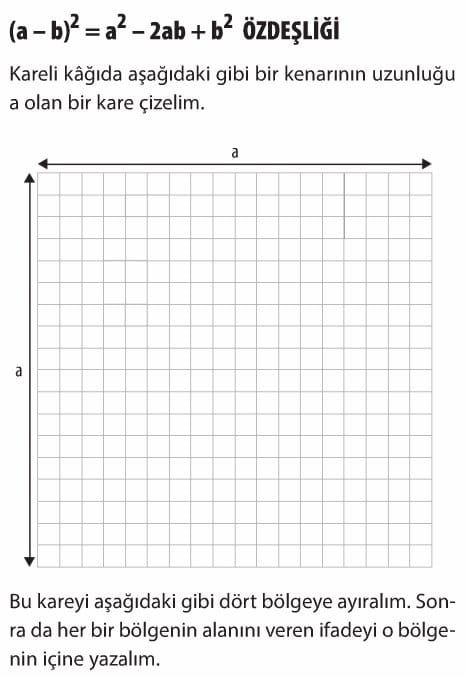
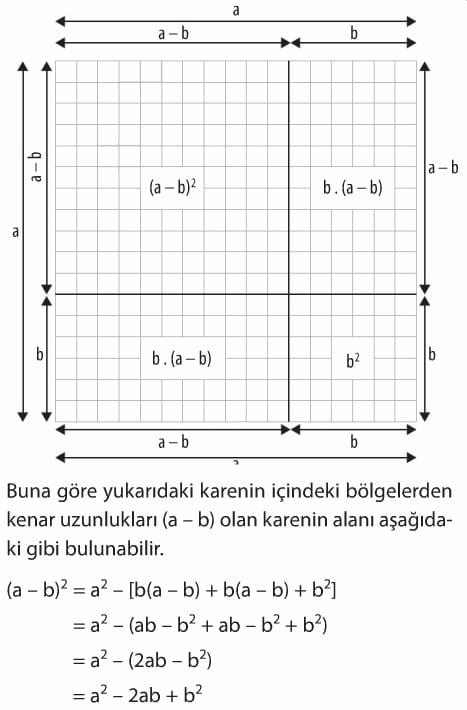
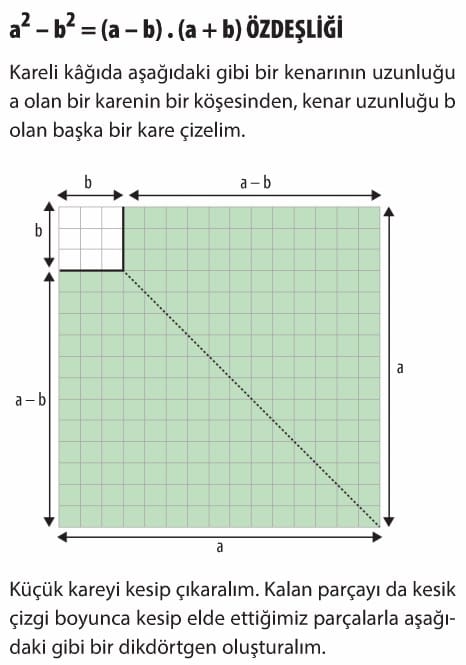
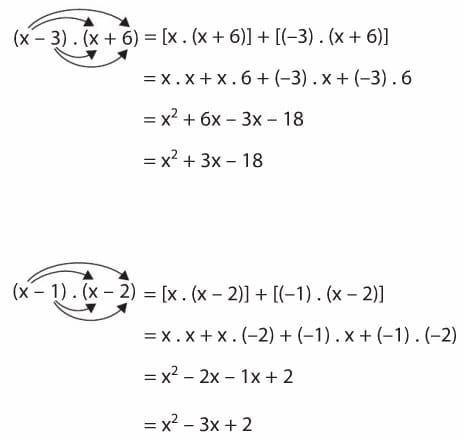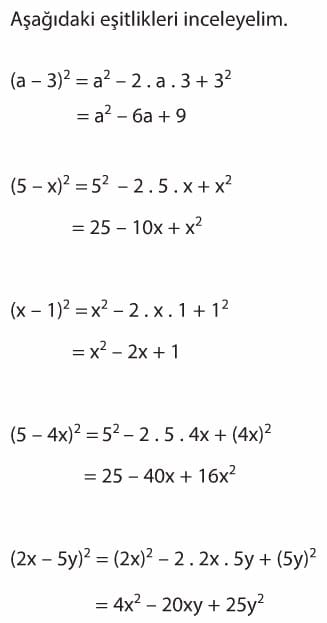Cebirsel İfadeler ve Özdeşlikler 8. Sınıf

Cebirsel İfadeler ve Özdeşlikler

En az bir bilinmeyen (değişken) ve işlem içeren ifadeler cebirsel ifadelerdir. x2, x+ 1, 3x – 2 ifadeleri birer cebirsel ifadedir.

CEBİRSEL İFADENİN ANLAMI

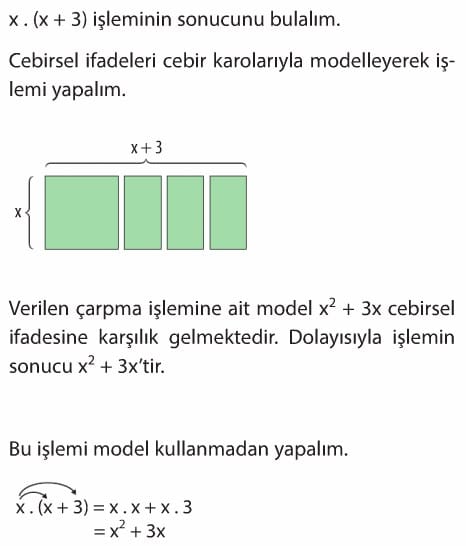
Santimetre cinsinden kenar uzunluklarıyla verilen dikdörtgensel bölgenin alanını hesaplayalım.

Cebirsel ifadede bir sayı ile değişkenin veya birden fazla değişkenin çarpımına terim denir. Yanında değişken olmayan terim, sabit terim olarak adlandırılır. Terimlerin sayısal çarpanı ise kat sayı olarak adlandırılır.

CEBİRSEL İFADELERLE ÇARPMA İŞLEMİ

İki terimli iki cebirsel ifade çarpılırken çarpma işleminin toplama veya çıkarma işlemleri üzerine dağılma özelliği uygulanır. Buna göre birinci ifadenin her iki terimi sırasıyla ikinci ifadenin birinci ve ikinci terimleriyle çarpılır.

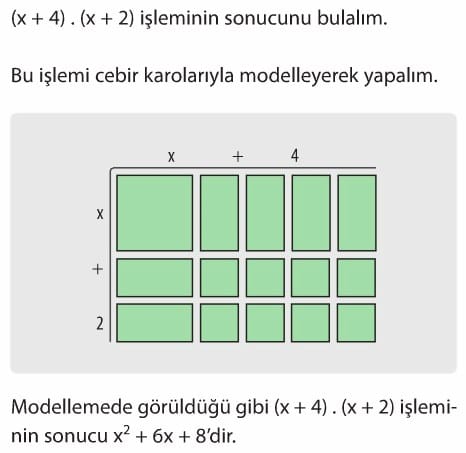
(x + 4) . (x + 2) işlemi çarpma işleminin toplama veya çıkarma işlemi üzerine dağılma özelliğinden yararlanılarak model kullanmadan aşağıdaki gibi yapılabilir.

Özdeşlikler

ÇARPANLARA AYIRMA

Bir harfli ifadeyi çarpanlarına ayırmak, çarpımları o harfli ifadeyi veren çarpanları bulmaktır. Çarpma işleminin toplama veya çıkarma işlemi üzerine dağılma özelliği ile özdeşliklerden yararlanarak harfli ifadeleri çarpanlarına ayırabiliriz. Örneğin x gibi bir ifadeyi x = k. m biçiminde yazmak x’i çarpanlarına ayırma işlemidir. Harfli ifadelerin çarpanları aşağıdaki yöntemlerden uygun olan kullanılarak bulunur.

  • Ortak çarpan parantezine alma
  • Özdeşliklerden yararlanma

Ortak çarpan Parantezine Alarak çarpanlara Ayırma

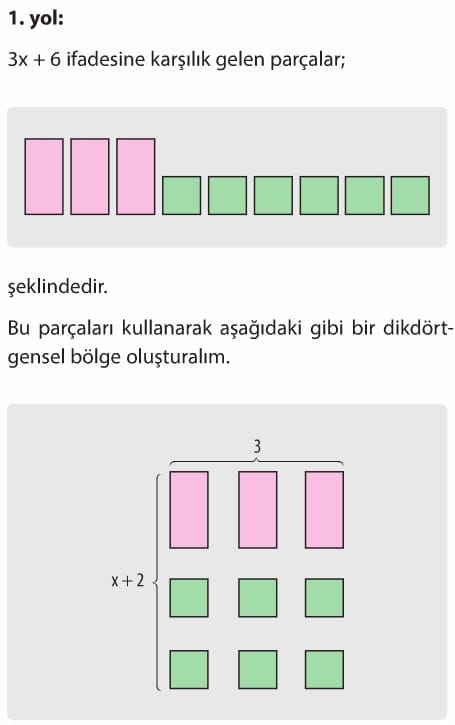
3x + 6 ifadesinin çarpanlarını bulalım. 3x + 6 ifadesinin çarpanlarını iki farklı yolla bulalım.

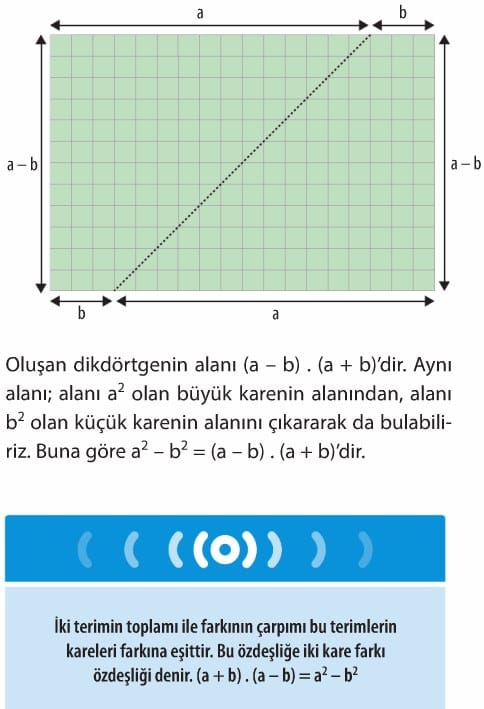
İki Kare Farkı Şeklinde Olan Bir İfadeyi Çarpanlarına Ayırma

Tam Kare Şeklinde Olan Bir İfadeyi Çarpanlarına Ayırma

ETİKETLER: , , ,
BİR YORUM YAZIN

ZİYARETÇİ YORUMLARI - 0 YORUM

Henüz yorum yapılmamış.

Cebirsel İfadeler ve Özdeşlikler konu anlatımı 8.sınıf çözümlü sorular

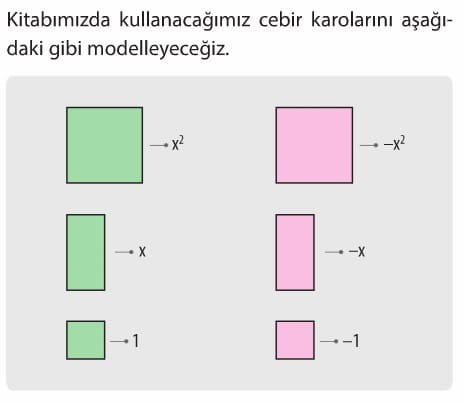
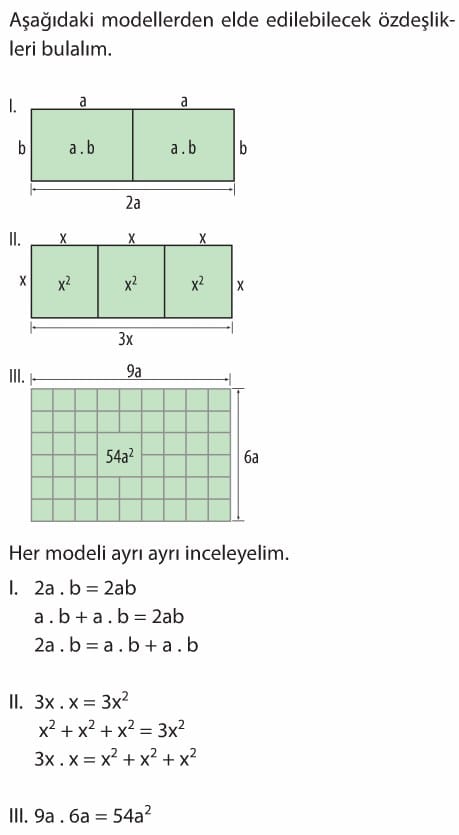
Kitabımızda kullanacağımız cebir karolarını aşağıdaki gibi modelleyeceğiz. Görüldüğü üzere eşitliğin sol tarafı düzenlendiğinde, eşitliğin sağ tarafındaki ifade elde edilir. Bu nedenle eşitlik x değişkenine verilecek bütün gerçek sayılar için sağlanır. Aşağıdaki ifadelerden hangilerinin özdeşlik olduğunu belirleyelim,
l. -2x+7:3x-8
ll. 3(2a + 5) = 15 + 6a
III. 2x(x - 1) -2x + 2x7
İfadeleri ayrı ayrı inceleyelim.
l. -2x + 7 = 3›< - 8 eşitliğinde x'in değerini bulalım.
-2x + 7 = 3x - 8 eşitliği sadece x = 3 için doğru olduğundan bir denklemdir.
II. 3(2a + 5): 15 + 6a eşitliğinde eşitliğin sol tarafını düzenleyelim.
3(2a+5)=3.2a+3.5=6a+15
Eşitliğin her iki tarafında da aynı cebirsel ifade vardır. 3(2a + 5) = 15 + 6a eşitliği, a yerine yazılacak bütün gerçek sayı değerleri için doğru olduğundan bir özdeşliktir.
III. 2x(x - 1) = - 2x + 2x2 eşitliğinde eşitliğin sol tarafını düzenleyelim.
2x(x-1)=2x.x-2x.1=2x2-2x
Eşitliğin her iki tarafında da aynı cebirsel ifade vardır. 2x(x - 1) = -2x + 2x2 eşitliği, x yerine yazılacak bütün gerçek sayı değerleri için doğru olduğundan bir özdeşliktir.