11. Sınıf Çarpışmalar Ders Notu

Çarpışma, birden fazla cismin esnek veya esnek olmayan etkileşimidir. Bir çarpışmada çarpışma türü ne olursa olsun, çarpışma öncesi momentumlar toplamı çarpışma sonrası momentumlar toplamına eşittir. Yani her koşulda momentum korunur.

Çarpışmalar iki kısımda incelenirler.
A) Bir boyutta çarpışmalar
B) İki boyutta çarpışmalar

A) Bir Boyutta çarpışmalar

Çarpışan cisimlerin hareket doğrultusu, cisimlerin merkezlerini birleştiren doğru üzerinde ise bu tür çarpışmalara bir boyutta (merkezi) çarpışmalar denir. Çarpışmalarda enerji korunumu varsa, bu çarpışmalara esnek çarpışmalar, enerji korunumu yok ise esnek olmayan çarpışmalar denir.

1. Merkezi esnek çarpışmalar

Merkezi çarpışmalar

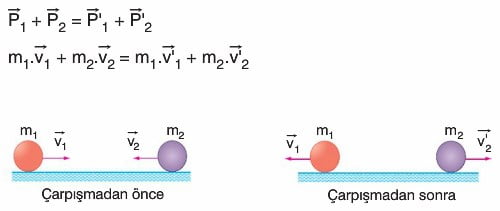
Çarpışmalarda Kinetik Enerjinin Korunumu

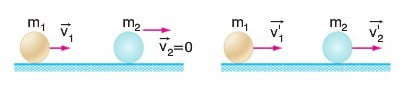
Çarpışmalar, kinetik enerjinin korunumuna göre iki kısma ayrılır. Kinetik enerjinin korunduğu çarpışmalara esnek çarpışmalar denir. İki cismin esnek çarpışmasında, çarpışma öncesi toplam kinetik enerji, çarpışma sonrası toplam kinetik enerjiye eşit olur. (Sürtünmeler önemsizdir.) Böylece;

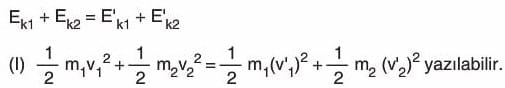
İki cismin esnek ve merkezi çarpışmasında momentumun korunumu da göz önüne alınırsa:

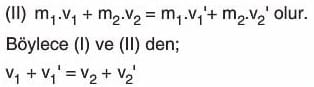
bulunabilir. m₂ kütleli cisim, çarpışmadan önce duruyorsa, cisimlerin çarpışmadan sonraki hızları:

Özel Durumlar

1. Çarpışan cisimlerin kütleleri eşit ise, çarpışma sonrası hızlarını birbirlerine aktarırlar (m1=m2)

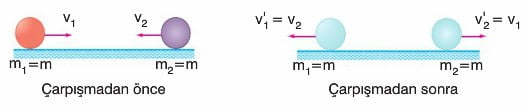
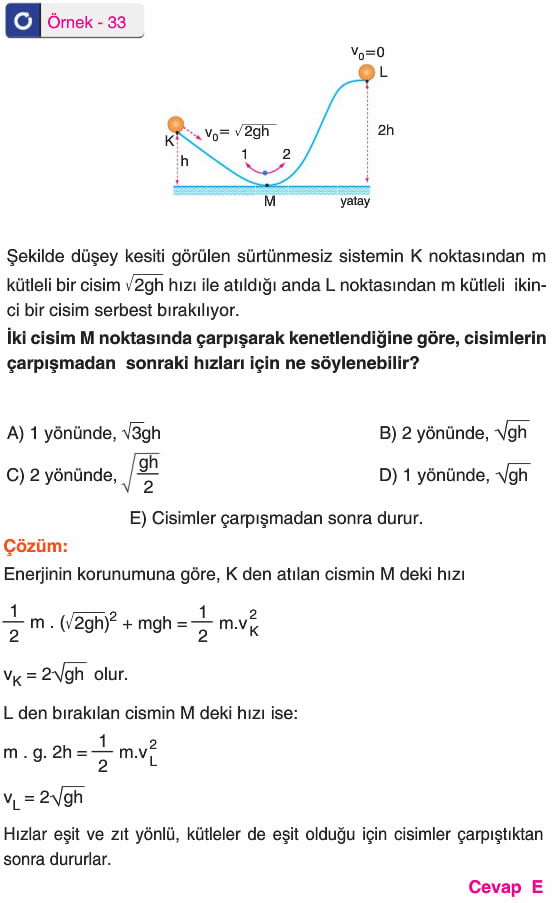
2. Çarpışan cisimlerin momentumları eşit şiddette ve zıt yönlü ise, çarpışma sonrası geldikleri doğrultuda geldikleri hızla geri dönerler.

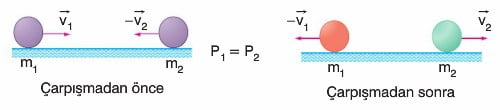
2. Merkezi esnek olmayan çarpışmalar

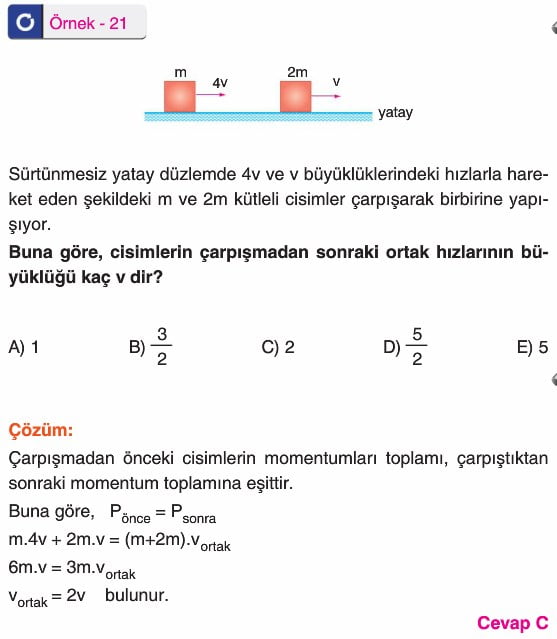
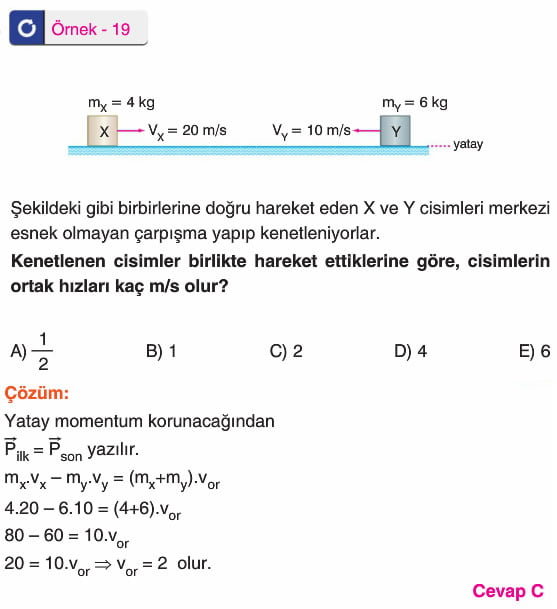
Cisimler çarpıştıktan sonra birlikte hareket ediyorlarsa, momentumun korunumu yazılarak cisimlerin ortak hızı bulunabilir.

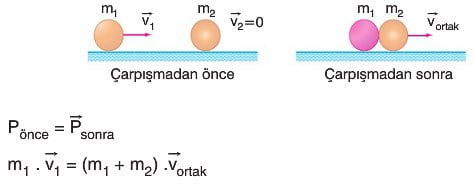
elde edilir. Bu tür çarpışmalara esnek olmayan çarpışmalar olarak bilinir.

Çözümlü Sorular

B) İki Boyutta çarpışmalar

Kütlesi ve hızı olan cisimlerin farklı doğrultuda hareket ederek çarpışmalarına iki boyutta çarpışma denir. Çarpışmalarda her durumda momentum korunur. Çarpışmalarda enerji korunumu var ise bu çarpışmalara iki boyutta esnek çarpışma, enerji korunumu yok ise bu tür çarpışmalara iki boyutta esnek olmayan çarpışma denir.

1) İki boyutta esnek çarpışmalar

Bir cisim duran bir cisme merkezi olmayan bir doğrultuda çarparsa cisimler farklı doğrultuda saçılır. Çarpışma öncesi toplam momentum çarpışma sonrası toplam momentuma eşittir.

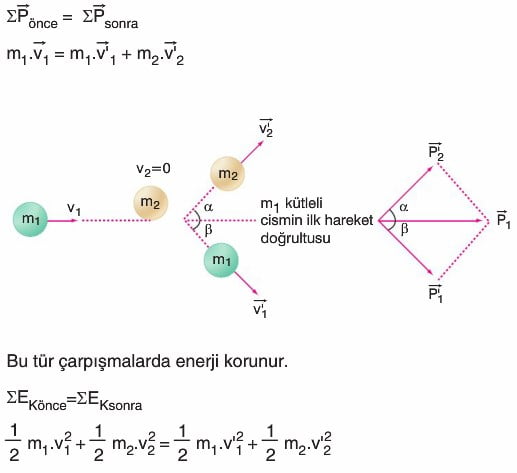
Not: Eğer cisimlerin kütleleri eşit ise, iki cisim çarpışmadan sonra aralarındaki açı 90^o olacak şekilde saçılırlar.

Yani α + β = 90^o

2) İki boyutta esnek olmayan çarpışmalar

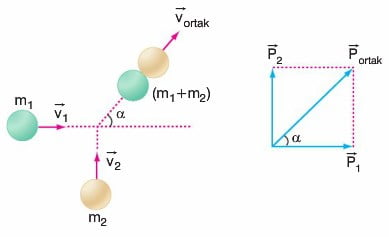
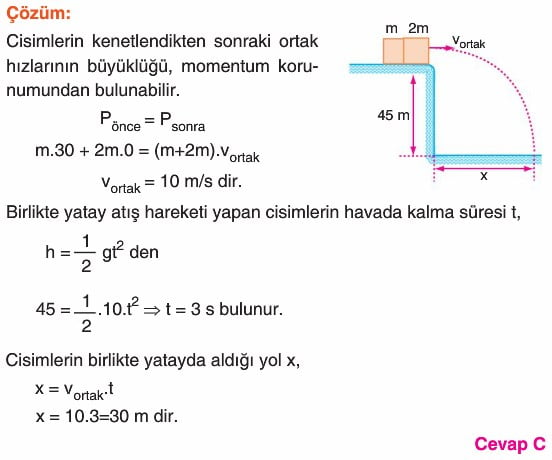
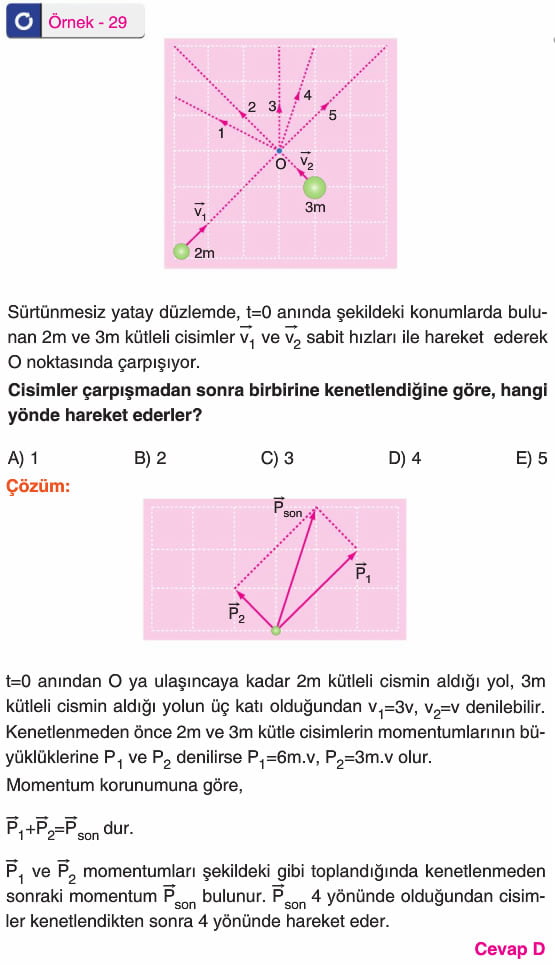
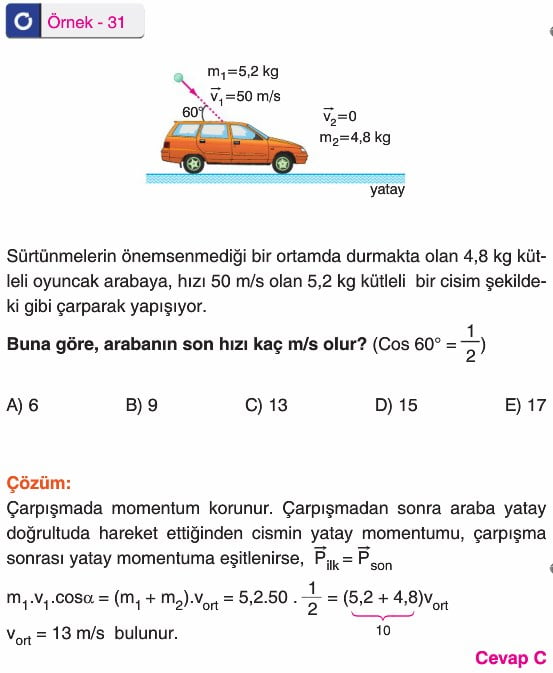
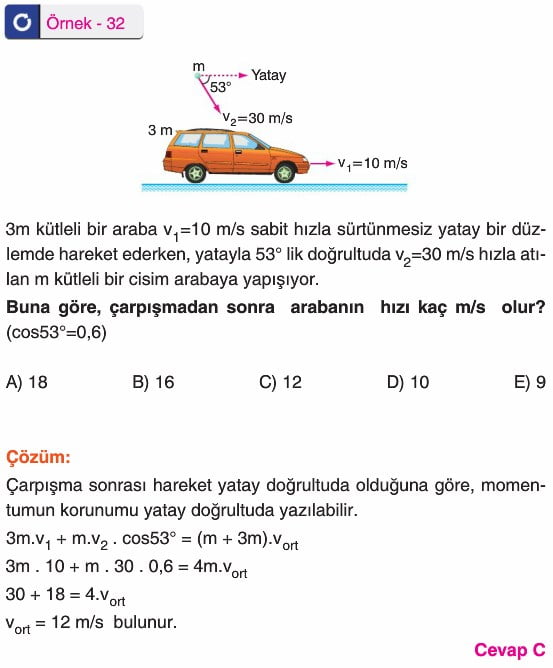
Cisimler çarpışmadan sonra kenetlenerek birlikte hareket edebilirler. Momentumun korunumundan yararlanılarak cisimlerin ortak hızı bulanabilir.

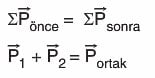
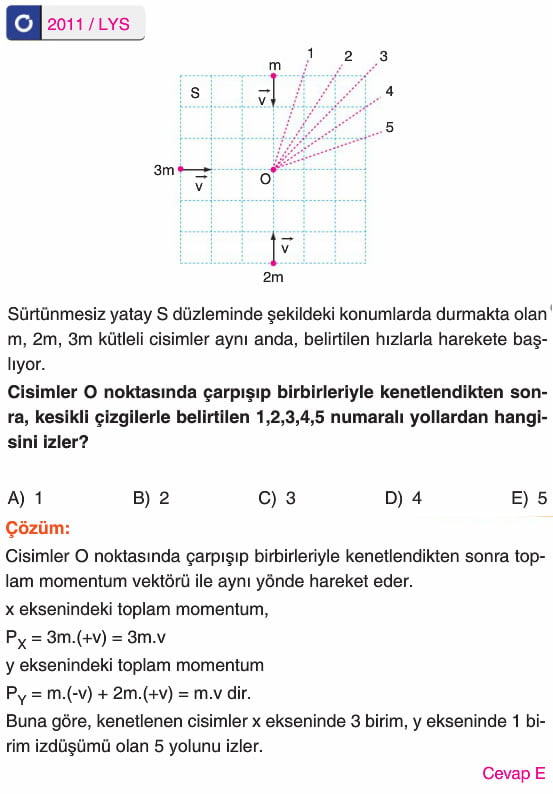
Bu tür çarpışmalarda enerji korunmaz. Çarpışma sonrası ortak kütlenin hızı, daima çarpışma öncesi momentumlarının vektörel toplamının yönünde olur.

Çözümlü Sorular

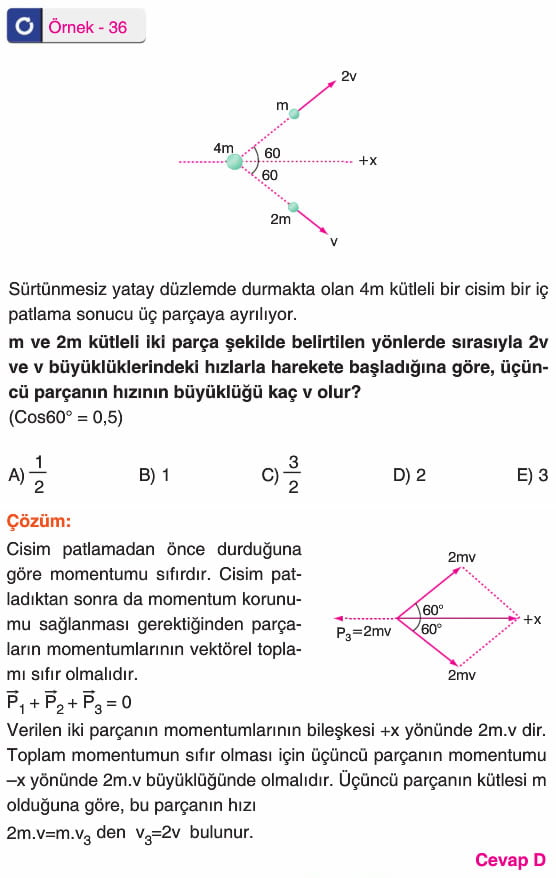
1) Duran cismin içten patlaması

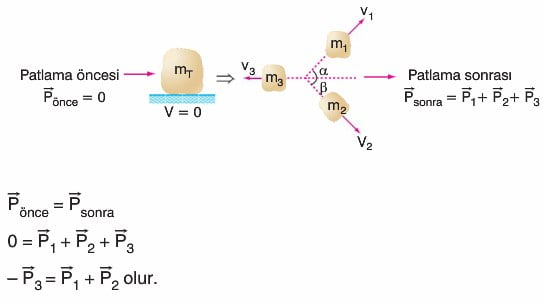
Çözümlü Sorular

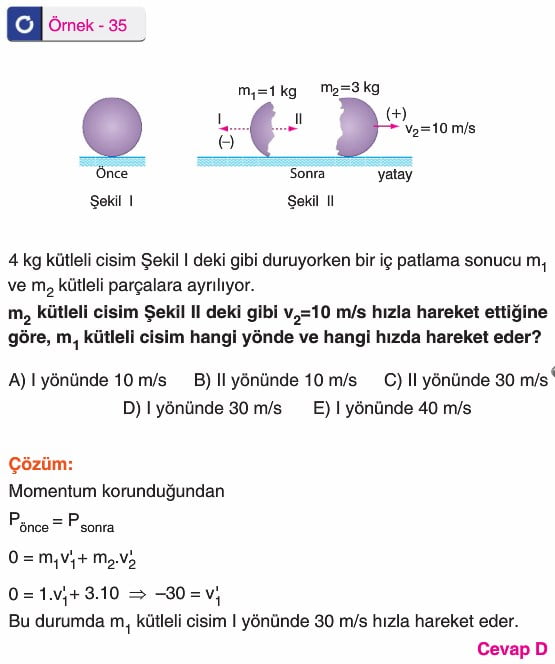
2)Hareket halindeki cismin içten patlaması

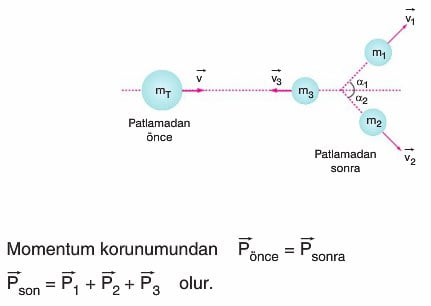
Çözümlü Sorular

Çözümlü Örnek Test Soruları: Çarpışmalar

• v₁ = Çarpışma öncesi hız
• v₁’ = Çarpışma sonrası hız

Soru 1

Durgun bir masa üzerinde duran 4 kg kütleli bir cisim, 2 m/s hızla gelen 2 kg kütleli bir cisimle esnek çarpışma yapıyor. Çarpışmadan sonra 4 kg kütleli cismin hızını bulunuz.

A) 0,5 m/s
B) 1 m/s
C) 1,5 m/s
D) 2 m/s

Çözüm:
Esnek çarpışmada hem momentum hem de kinetik enerji korunur. Öncelikle momentum korunumu denklemini yazıyoruz:

m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’

Başlangıçta:

• m₁ = 4 kg (4 kg’lık cisim)
• v₁ = 0 (4 kg’lık cisim duruyor)
• m₂ = 2 kg (çarpan cisim)
• v₂ = 2 m/s

Çarpışmadan sonra hızlar:

• v₁’ (4 kg’lık cismin hızı, arıyoruz)
• v₂’ (2 kg’lık cismin hızı, arıyoruz)

Momentum korunumu:
4(0) + 2(2) = 4v₁’ + 2v₂’
4 = 4v₁’ + 2v₂’ …(1)

Enerji korunumu (esnek çarpışma):
0,5 × 4 × (0²) + 0,5 × 2 × (2²) = 0,5 × 4 × (v₁’)² + 0,5 × 2 × (v₂’)²
0 + 4 = 2(v₁’)² + (v₂’)² …(2)

Bu iki denklem çözülerek:
v₁’ = 1 m/s bulunur.
Doğru cevap: B

---

Soru 2

2 m/s hızla hareket eden 3 kg kütleli bir cisim, durmakta olan 1 kg kütleli bir cisme çarpıyor. Çarpışma tamamen esnektir. Çarpışmadan sonra 1 kg kütleli cismin hızı kaç olur?

A) 1 m/s
B) 2 m/s
C) 3 m/s
D) 4 m/s

Çözüm:
Momentum ve kinetik enerji korunur. Önce momentum denklemimizi yazıyoruz:

m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’

Başlangıçta:

• m₁ = 3 kg, v₁ = 2 m/s (ilk cisim)
• m₂ = 1 kg, v₂ = 0 (ikinci cisim duruyor)

Son hızlar:

• v₁’ ve v₂’ (çarpışma sonrası hızlar)

Momentum denklemi:
3(2) + 1(0) = 3v₁’ + 1v₂’
6 = 3v₁’ + v₂’ …(1)

Enerji korunumu:
0,5 × 3 × (2²) + 0,5 × 1 × (0²) = 0,5 × 3 × (v₁’)² + 0,5 × 1 × (v₂’)²
6 = 1,5(v₁’)² + 0,5(v₂’)² …(2)

Bu iki denklem çözüldüğünde:
v₂’ = 3 m/s bulunur.
Doğru cevap: C

---

Soru 3

5 kg kütleli bir cisim, 1 m/s hızla 2 kg kütleli başka bir cisme çarpıyor. Çarpışma sonucunda 5 kg kütleli cismin hızı duruyor. 2 kg kütleli cismin hızı ne olur?

A) 1,5 m/s
B) 2 m/s
C) 2,5 m/s
D) 3 m/s

Çözüm:
Momentum korunumu:

m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’

Başlangıçta:

• m₁ = 5 kg, v₁ = 1 m/s (ilk cisim)
• m₂ = 2 kg, v₂ = 0 (ikinci cisim duruyor)

Son hızlar:

• v₁’ = 0 (ilk cismin hızı duruyor)
• v₂’ (ikinci cismin son hızı, arıyoruz)

Momentum denklemi:
5(1) + 2(0) = 5(0) + 2v₂’
5 = 2v₂’
v₂’ = 2,5 m/s

Doğru cevap: C

---

Soru 4

Bir masa üzerinde duran 3 kg kütleli bir cisim, 4 m/s hızla gelen 6 kg kütleli başka bir cisimle esnek çarpışma yapıyor. Çarpışmadan sonra 3 kg kütleli cismin hızı nedir?

A) 2 m/s
B) 3 m/s
C) 4 m/s
D) 5 m/s

Çözüm:
Momentum denklemini yazıyoruz:

m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’

Başlangıçta:

• m₁ = 3 kg, v₁ = 0 (ilk cisim duruyor)
• m₂ = 6 kg, v₂ = 4 m/s (ikinci cisim)

Sonuçta:

• v₁’ (ilk cismin son hızı, arıyoruz)
• v₂’ (ikinci cismin son hızı, arıyoruz)

Momentum korunumu:
3(0) + 6(4) = 3v₁’ + 6v₂’
24 = 3v₁’ + 6v₂’ …(1)

Enerji korunumu:
0,5 × 3 × (0²) + 0,5 × 6 × (4²) = 0,5 × 3 × (v₁’)² + 0,5 × 6 × (v₂’)²
48 = 1,5(v₁’)² + 3(v₂’)² …(2)

Bu iki denklem çözüldüğünde:
v₁’ = 5 m/s bulunur.
Doğru cevap: D

---

Soru 5

10 m/s hızla hareket eden 2 kg kütleli bir cisim, durmakta olan 8 kg kütleli bir cisme çarptıktan sonra duruyor. 8 kg kütleli cismin hızı kaç olur?

A) 2,5 m/s
B) 5 m/s
C) 7,5 m/s
D) 10 m/s

Çözüm:
Momentum denklemini yazıyoruz:

m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’

Başlangıçta:

• m₁ = 2 kg, v₁ = 10 m/s
• m₂ = 8 kg, v₂ = 0

Sonuçta:

• v₁’ = 0 (ilk cismin son hızı sıfır)
• v₂’ (ikinci cismin son hızı, arıyoruz)

Momentum korunumu:
2(10) + 8(0) = 2(0) + 8v₂’
20 = 8v₂’
v₂’ = 2,5 m/s

Doğru cevap: A