Birinci Dereceden İki Bilinmeyenli Eşitsizlik Sistemleri 9. Sınıf

Eşitsizlik Sistemi

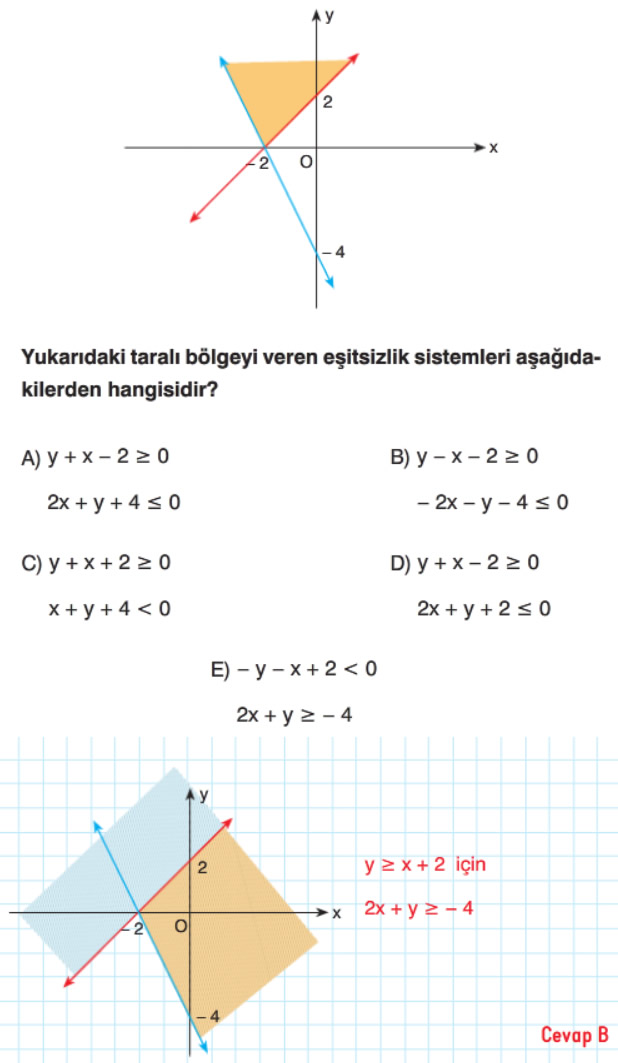
Çözümlü Sorular
Birinci Dereceden İki Bilinmeyenli Eşitsizlik Sistemleri 9. sınıf matematik soru çözümleri konu anlatımı
a, b ve c sabit gerçek sayılar ve a ve b sıfırdan farklı olmak üzere, ax + by ≤ c şeklinde yazılan ifadelere birinci dereceden iki bilinmeyenli eşitsizlik denir. ≤ sembolü yerine >, <, veya ≥ sembolleri de yazılabilir.)
Bir eşitsizliği sağlayan (x, y) sıralı ikilisine o eşitsizliğin bir çözümü denir. Eşitsizliği sağlayan bütün sıralı ikililere ise eşitsizliğin çözüm kümesi denir ve grafik üzerinde taralı bölge olarak gösterilir.
Eşitsizliklerin Grafik Çizimi
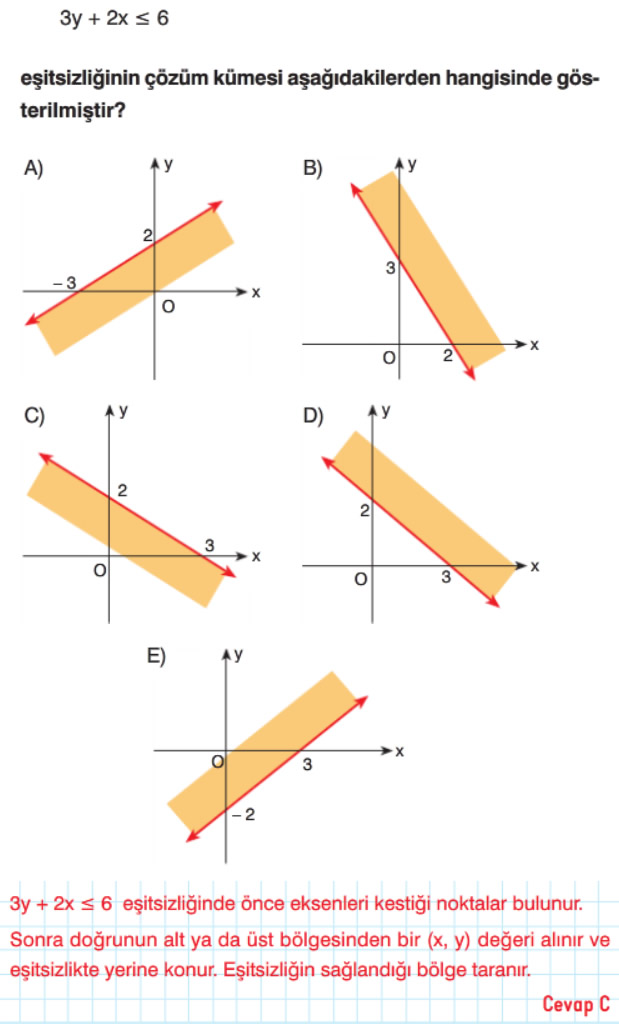
- Eşitsizlik sembolünü "=" sembolüne çevirerek bir denklem elde edilir. Bu denklemin grafiği çizilir. <, > sembolleri için kesikli çizgi, ≥, ≤ sembolleri için grafik düz çizgi olarak çizilir.
- Denklem grafiğinin iki bölgeye ayırdığı koordinat düzleminin herhangi bir tarafından bir nokta alınıp eşitsizlikte yerine koyarak sağlayıp sağlamadığını kontrol edilir.
- Genel olarak doğrunun grafiği orijinden geçmiyorsa, (0, 0) noktası test noktası olarak alınabilir.
- Test edilen nokta eşitsizliği sağlıyorsa noktanın bulunduğu bölge, sağlamıyorsa diğer bölge taranır.
Denklem sistemlerinde olduğu gibi, değişkenleri aynı olan birden fazla eşitsizliğe eşitsizlik sistemi denir. Eşitsizlik sisteminin çözüm kümesinde bulunan (x, y) sıralı ikililerinin, ortak bir çözüm olması için sistemde bulunan her eşitsizliği sağlamalıdır.
Eşitsizlik Türleri:
Doğrusal Eşitsizlikler: Bir bilinmeyenin birinci dereceden polinomla ifade edildiği eşitsizliklerdir. Genel formül şu şekildedir: ax + b < c veya ax + b > c gibi.
Mutlak Değer Eşitsizlikleri: |ax + b| < c veya |ax + b| > c gibi ifadeleri içeren eşitsizliklerdir.
Karekök Eşitsizlikleri: √(ax + b) < c veya √(ax + b) > c gibi eşitsizliklerdir.
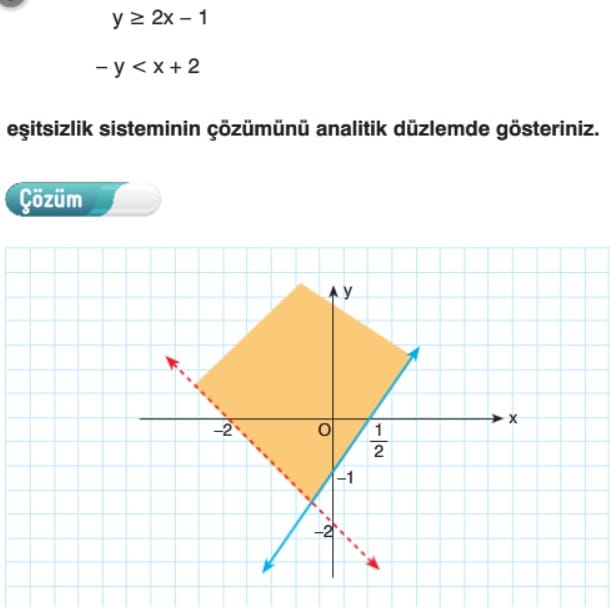
- Her bir eşitsizliği tek başına çözerek çözüm kümesini bulalım.
- Çözüm kümelerini birleştirerek eşitsizlik sisteminin genel çözüm kümesini bulalım.
- İki eşitsizliğin çözüm kümeleri aynı ise, eşitsizlik sisteminin çözüm kümesi bu kümedir.
- İki eşitsizliğin çözüm kümeleri kesişimsiz ise, eşitsizlik sisteminin çözüm kümesi boş kümedir.
- İki eşitsizliğin çözüm kümeleri bir noktada kesişiyorsa, eşitsizlik sisteminin çözüm kümesi bu noktadır.