Birinci Dereceden İki Bilinmeyenli Eşitsizlik Sistemleri Test 1 Çöz

Birinci Dereceden İki Bilinmeyenli Eşitsizlik Sistemleri Çözümlü Sorular

Çözümlü Örnek Test Soruları

1. Aşağıdaki eşitsizlik sisteminin çözüm kümesini sağlayan noktayı bulunuz.

x + y ≤ 5
2x – y > 1

A) (2,2)
B) (3,1)
C) (1,3)
D) (0,4)

Çözüm:

1. x + y = 5 doğrusunun kesişim noktaları:

   • x = 0 için y = 5
   • y = 0 için x = 5

2. 2x – y = 1 doğrusunun kesişim noktaları:

   • x = 0 için y = -1
   • y = 0 için x = 0.5

Şimdi verilen noktaları inceleyelim:

A) (2,2) → 2 + 2 = 4 ≤ 5, 2(2) – 2 = 2 > 1 (Doğru)
B) (3,1) → 3 + 1 = 4 ≤ 5, 2(3) – 1 = 5 > 1
C) (1,3) → 1 + 3 = 4 ≤ 5, 2(1) – 3 = -1 > 1
D) (0,4) → 0 + 4 = 4 ≤ 5, 2(0) – 4 = -4 > 1

Doğru cevap: A) (2,2)

---

2. Aşağıdaki eşitsizlik sisteminin çözüm kümesini sağlayan noktayı bulunuz.

2x – y ≥ 3
x + 2y < 6

A) (1,1)
B) (2,2)
C) (3,0)
D) (0,3)

Çözüm:

1. 2x – y = 3 doğrusunun kesişim noktaları:

   • x = 0 için y = -3
   • y = 0 için x = 1.5

2. x + 2y = 6 doğrusunun kesişim noktaları:

   • x = 0 için y = 3
   • y = 0 için x = 6

Şimdi noktaları inceleyelim:

A) (1,1) → 2(1) – 1 = 1 ≥ 3 değil
B) (2,2) → 2(2) – 2 = 2 ≥ 3 değil
C) (3,0) → 2(3) – 0 = 6 ≥ 3, 3 + 2(0) = 3 < 6 (Doğru)
D) (0,3) → 2(0) – 3 = -3 ≥ 3 değil

Doğru cevap: C) (3,0)

---

3. Aşağıdaki eşitsizlik sisteminin çözüm kümesini sağlayan noktayı bulunuz.

x – y ≤ 2
3x + y > 4

A) (1,2)
B) (2,1)
C) (0,0)
D) (3,2)

Çözüm:

1. x – y = 2 doğrusunun kesişim noktaları:

   • x = 0 için y = -2
   • y = 0 için x = 2

2. 3x + y = 4 doğrusunun kesişim noktaları:

   • x = 0 için y = 4
   • y = 0 için x = 4/3

Şimdi noktaları inceleyelim:

A) (1,2) → 1 – 2 = -1 ≤ 2, 3(1) + 2 = 5 > 4 (Doğru)
B) (2,1) → 2 – 1 = 1 ≤ 2, 3(2) + 1 = 7 > 4
C) (0,0) → 0 – 0 = 0 ≤ 2, 3(0) + 0 = 0 > 4 değil
D) (3,2) → 3 – 2 = 1 ≤ 2, 3(3) + 2 = 11 > 4

Doğru cevap: A) (1,2)

---

4. Aşağıdaki eşitsizlik sisteminin çözüm kümesini sağlayan noktayı bulunuz.

y < 2x + 3
y ≥ x – 1

A) (1,3)
B) (2,4)
C) (3,2)
D) (0,2)

Çözüm:

1. y = 2x + 3 doğrusunun kesişim noktaları:

   • x = 0 için y = 3
   • y = 0 için x = -1.5

2. y = x – 1 doğrusunun kesişim noktaları:

   • x = 0 için y = -1
   • y = 0 için x = 1

Şimdi noktaları inceleyelim:

A) (1,3) → 3 < 2(1) + 3 değil
B) (2,4) → 4 < 2(2) + 3 değil
C) (3,2) → 2 < 2(3) + 3, 2 ≥ 3 – 1 (Doğru)
D) (0,2) → 2 < 2(0) + 3, 2 ≥ 0 – 1

Doğru cevap: C) (3,2)

---

5. Aşağıdaki eşitsizlik sisteminin çözüm kümesini sağlayan noktayı bulunuz.

y ≤ x + 4
y > 2x – 1

A) (1,2)
B) (2,3)
C) (3,5)
D) (0,0)

Çözüm:

1. y = x + 4 doğrusunun kesişim noktaları:

   • x = 0 için y = 4
   • y = 0 için x = -4

2. y = 2x – 1 doğrusunun kesişim noktaları:

   • x = 0 için y = -1
   • y = 0 için x = 0.5

Şimdi noktaları inceleyelim:

A) (1,2) → 2 ≤ 1 + 4, 2 > 2(1) – 1 (Doğru)
B) (2,3) → 3 ≤ 2 + 4, 3 > 2(2) – 1 değil
C) (3,5) → 5 ≤ 3 + 4, 5 > 2(3) – 1 değil
D) (0,0) → 0 ≤ 0 + 4, 0 > 2(0) – 1

Doğru cevap: A) (1,2)

---

ax + by + c = 0 doğrusunun düzlemde ayırdığı açık ya da kapalı yarı düzlemler aşağıdaki gibi gösterilir.

Açık Yarı Düzlemler
ax + by + c > 0
ax + by + c < 0

Kapalı Yarı Düzlemler
ax + by + c ≥ 0
ax + by + c ≤ 0

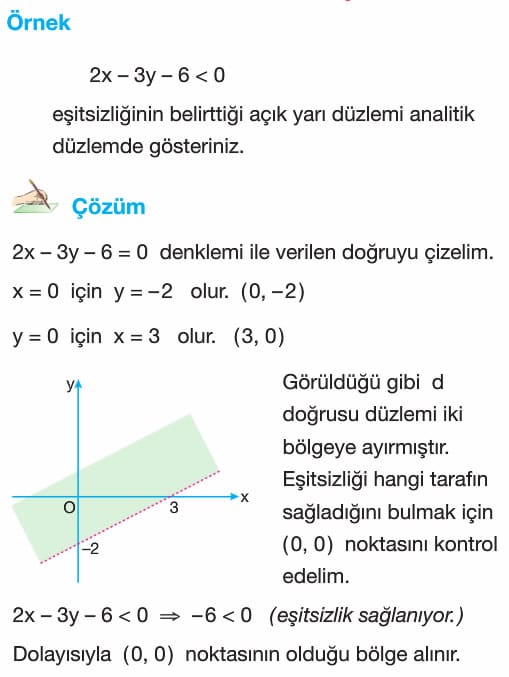
Örnek: 2x – 3y – 6 < 0 eşitsizliğinin belirttiği açık yarı düzlemi analitik düzlemde gösteriniz.
Çözüm: 2x – 3y – 6 = 0 denklemi ile verilen doğruyu çizelim.
x=0 için y=-2 ve y = 0 için x = 3 olur. (0,-2) ve (3,0) noktaları
Görüldüğü gibi d doğrusu düzlemi iki bölgeye ayırmıştır. Eşitsizliği hangi bölgenin sağladığını bulmak için (0,0) başlangıç noktasını kontrol edelim.
2x – 3y – 6 < 0 ise -6 < 0 (Eşitsizlik sağlanıyor)
Dolayısıyla (0,0) noktasının olduğu bölge alınır.

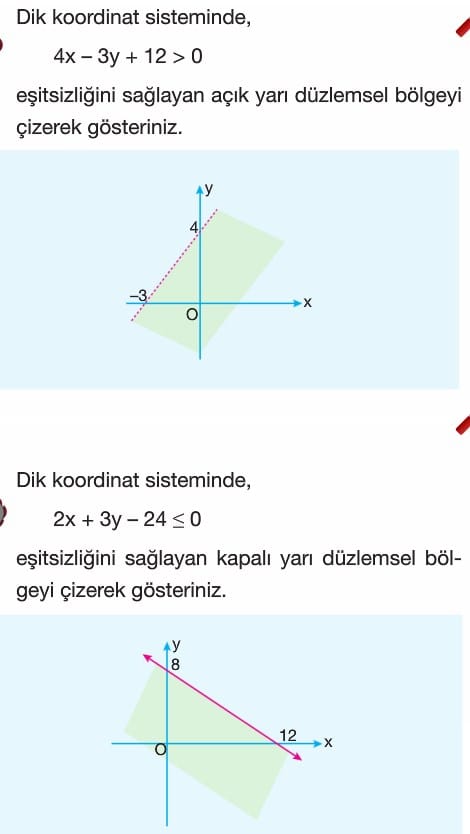
Soru: Dik koordinat sisteminde, 4x – 3y + 12 > 0 eşitsizliğini sağlayan açık yarı düzlemsel bölgeyi çizerek gösteriniz.
Soru: Dik koordinat sisteminde, 2x+3y-24 < 0 eşitsizliğini sağlayan kapalı yarı düzlemsel bölgeyi çizerek gösteriniz.
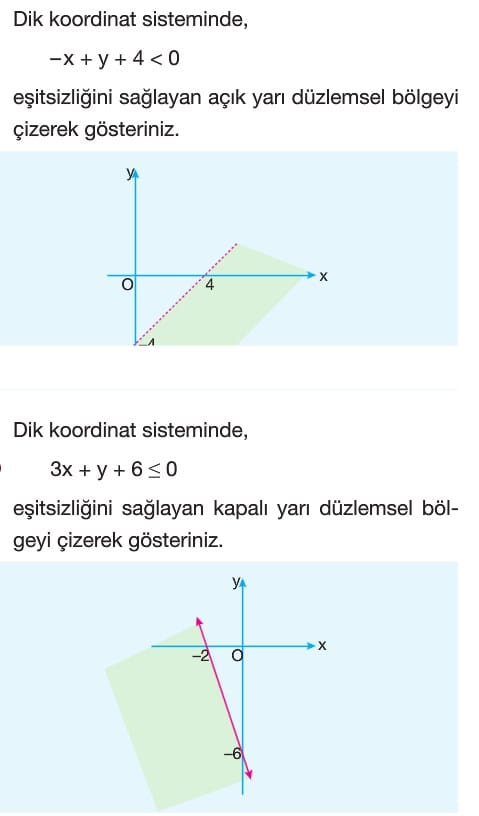
Soru: Dik koordinat sisteminde, -x + y + 4 < 0 eşitsizliğini sağlayan açık yarı düzlemsel bölgeyi çizerek gösteriniz.
Soru: Dik koordinat sisteminde, 3x + y + 6 < 0 eşitsizliğini sağlayan kapalı yarı düzlemsel bölgeyi çizerek gösteriniz.

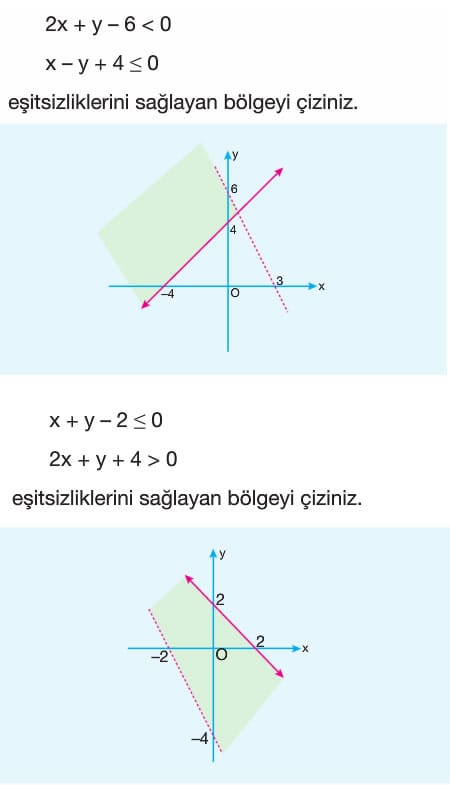
Örnek: x + y + 2 < 0
y – x + 1> 0
eşitsizliklerini sağlayan bölgeyi bulunuz.
Çözüm: y — x + 1 = 0 doğrusunu çizelim.
x = 0 için
y=-1 (0,-1)
y = 0 için
x =1 = (1,0)
(0, 0) noktasını y — x + 1 > 0 eşitsizliğinde yerine koyarsak 0 — 0 + 1 > 0 ise 1 > 0 sağladığı için (0, 0) noktasının bulunduğu bölge y — x + 1 > 0 eşitsizliğinin çözüm kümesidir.
x + y + 2 = O doğrusunu çizelim.
x = O için = y = —2   (O, —2)
y = O için = x = —2   (-2, O)
(0, 0) noktasını x + y + 2 < 0 eşitsizliğinde yerine koyarsak
O + O + 2 < 2 = 2 < O sağlamadığı için (O, O) noktasının bulunmadığı bölge x + y + 2 < 0 eşitsizliğinin çözüm kümesidir.
Her iki eşitsizliğin ortak bölgesi,
x + y + 2 < O ve y—x +1 >O eşitsizliklerini sağlayan bölgedir.