Birinci Dereceden iki Bilinmeyenli Denklemler 9. Sınıf
Bu yazımızda 9. sınıf müfredatında bulunan Birinci Dereceden iki Bilinmeyenli Denklemler konu anlatımı yer almaktadır. Konuyu bitirdikten sonra Birinci Dereceden iki Bilinmeyenli Denklemler soruları ve çözümleri yazımıza da bakabilirsiniz.
Birinci Dereceden iki Bilinmeyenli Denklemler Ders Notu
a, b ve c sabit gerçek sayılar, a ve b sıfırdan farklı olmak üzere, x ve y değişkenleri için ax + by = c şeklinde yazılan ifadelere birinci dereceden iki bilinmeyenli denklem denir.
Değişkenleri birinci dereceden ve aynı olan birden fazla denklem grubuna ise birinci dereceden iki bilinmeyenli denklem sistemi denir. Bir denklem sisteminin çözüm kümesi, bu iki denklemi aynı anda sağlayan (x, y) sıralı ikilileridir.


Çözümlü Sorular
1. Dereceden 2 Bilinmeyenli Denklem Sistemlerinin Çözüm Kümesi
Bir denklem sisteminin çözüm kümesini sıralı ikilileri tek tek yerine koyarak belirlemek her zaman mümkün olmayabilir. Denklem sistemlerinin çözümlerini bulmak için yerine koyma, yok etme, grafik çizme gibi matematiksel yöntemler kullanılır.
Yerine Koyma Yöntemi
ax + by = c
dx + ey = f
denklem sisteminin yerine koyma yöntemi ile çözümünde; birinci ya da ikinci denklemde x ya da y değişkeni yalnız bırakılarak, elde edilen ifade diğer denklemde yerine yazılır.
Yerine Koyma Yöntemiyle denklem sistemini çözerken genellikle katsayısı 1 olan değişken diğer değişken türünden ifade edilir.

Yok Etme Yöntemi
ax + by = c
dx + ey = f
denklem sisteminin yok etme yönteminde her iki denklem taraf tarafa toplanarak bilinmeyenlerden birisi yok edilir. Verilen denklem sisteminde taraf tarafa toplama işlemi ile bilinmeyenlerden birisi yok olmuyorsa, çarpma işlemi ile bilinmeyenlerden birisinin katsayıları eşit ve zıt işaretli olacak şekilde düzenlenir.

Not:


Birinci Dereceden iki Bilinmeyenli Denklem Sistemleri Soru ve Çözümleri
Çözümlü Sorular
Soru 1:
2x + y = 5
x – y = 1
denklem sistemini çözünüz.
Çözüm:
İkinci denklemden x = y + 1 bulunur.
Birinci denklemde yerine yazarsak:
2(y + 1) + y = 5
2y + 2 + y = 5
3y = 3
y = 1
x = 1 + 1 = 2
Çözüm: (2,1)
Soru 2:
3x + 2y = 8
x – y = 1
denklem sistemini çözünüz.
Çözüm:
İkinci denklemden x = y + 1
Birinci denklemde yerine yazarsak:
3(y + 1) + 2y = 8
3y + 3 + 2y = 8
5y = 5
y = 1
x = 1 + 1 = 2
Çözüm: (2,1)
Soru 3:
x + y = 4
2x – y = 5
denklem sistemini çözünüz.
Çözüm:
Denklemleri toplarsak:
3x = 9
x = 3
Birinci denklemde yerine yazarsak:
3 + y = 4
y = 1
Çözüm: (3,1)
Soru 4:
4x – y = 7
2x + 3y = 9
denklem sistemini çözünüz.
Çözüm:
Birinci denklemden y = 4x – 7
İkinci denklemde yerine yazarsak:
2x + 3(4x – 7) = 9
2x + 12x – 21 = 9
14x = 30
x = 30/14 = 15/7
y = 4(15/7) – 7 = 60/7 – 49/7 = 11/7
Çözüm: (15/7, 11/7)
Soru 5:
5x + 2y = 10
10x + 4y = 20
denklem sistemini çözünüz.
Çözüm:
İkinci denklem birinci denklemin 2 katı olduğundan sonsuz çözüm vardır.
Çözüm: (k, 5 – (5/2)k) (k ∈ R)
Soru 6:
x + 2y = 3
2x + 4y = 7
denklem sistemini çözünüz.
Çözüm:
İkinci denklem birinci denklemin 2 katı değildir (7 ≠ 6).
Denklemler paralel olduğundan çözüm yoktur.
Önemli Notlar:
- Denklemler kesişiyorsa tek çözüm vardır
- Denklemler aynı doğruyu gösteriyorsa sonsuz çözüm vardır
- Denklemler paralel ise çözüm yoktur
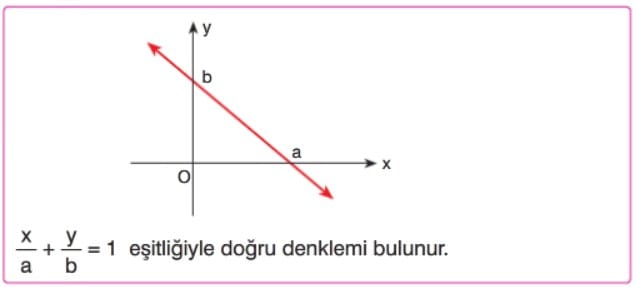
a, b, c ∈ R ve a ≠ 0, b ≠ 0 olmak üzere, ax + by + c = 0 biçiminde ifade edilen denklemlere birinci dereceden iki bilinmeyenli denklemler denir. Denklemi sağlayan (x, y) ikililerinin kümesine denklemin çözüm kümesi denir.
Grafik Çizme Yöntemi
y = mx + n şeklindeki bir ifadenin koordinat düzleminde eğimi m, y eksenini kestiği nokta n dir.
y = mx + n ve ax + by = c denklemlerin grafikleri koordinat düzleminde bir doğru belirtir. Denklem sistemlerinin grafiksel yorumunu yaparken denklem sisteminde bulunan her iki denklem y = mx + n şeklinde yazılır. Grafik çiziminde kolaylık olması için x yerine 0 yazıp y değeri ve y yerine 0 yazıp x değeri bulunur.
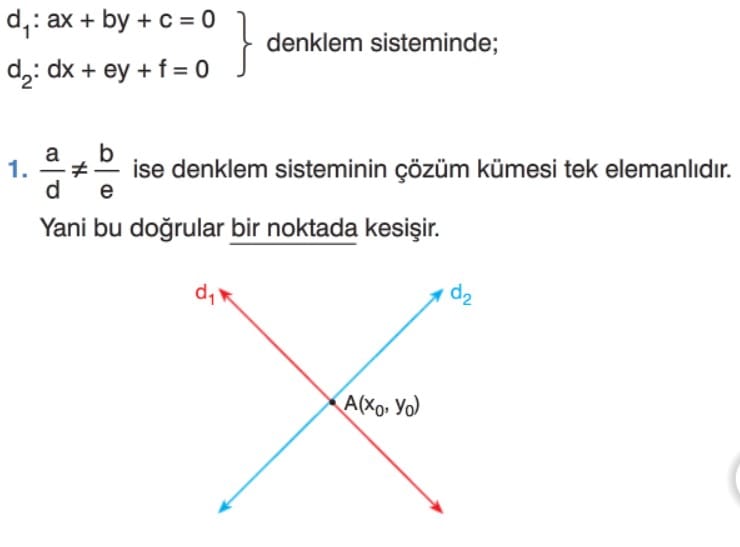
Bir denklem sisteminde;
- Doğrular kesişiyor ise çözüm kümesi (x, y) sıralı ikilisi şeklinde tek bir noktadan oluşur.
- Doğrular paralel ise çözüm kümesi boş kümedir.
- Doğrular çakışık ise sistemdeki her iki denklem de aynıdır. Denklemlerden birini sağlayan bütün sıralı ikililer çözüm kümesidir ve çözüm kümesi sonsuz elemanlıdır.





















