Bu yazımızda Birinci Dereceden İki Bilinmeyenli Denklemler (Denklem Sistemleri) Soru Çözümleri yer almaktadır. Konu ile ilgili bilgi eksikliğiniz var ise Birinci Dereceden İki Bilinmeyenli Denklemler Konu Anlatımı yazımıza da bakmanızı tavsiye ederiz.

Birinci Dereceden İki Bilinmeyenli Denklem Sistemleri Test 1 Çöz

Birinci Dereceden İki Bilinmeyenli Denklemler Çözümlü Sorular

Çözümlü Örnek Test Soruları

Soru 1:
Aşağıdaki denklemler sistemini çözünüz:
2x + 3y = 12
x – y = 1

A) (3, 2)
B) (4, 1)
C) (5, 0)
D) (2, 2)
E) (1, 3)

Çözüm:
İkinci denklemi kullanarak x = y + 1 elde edilir ve bu ifade birinci denklemde yerine konur:
2(y + 1) + 3y = 12
2y + 2 + 3y = 12
5y = 10
y = 2 bulunur ve x = y + 1 = 3 olur.
Doğru cevap: A) (3, 2)

Soru 2:
3x – 2y = 14 ve 2x + y = 9 denklemlerinin çözüm kümesi nedir?

A) (4, 1)
B) (3, 3)
C) (2, 5)
D) (5, -1)
E) (0, 7)

Çözüm:
İkinci denklemi y cinsinden çözerek y = 9 – 2x ifadesini birinci denklemde yerine koyarız:
3x – 2(9 – 2x) = 14
3x – 18 + 4x = 14
7x = 32 ve x = 4 bulunur.
Doğru cevap: A) (4, 1)

Soru 3:
Birinci dereceden iki bilinmeyenli aşağıdaki denklemler sistemini çözünüz:
x + y = 7
x – y = 3

A) (5, 2)
B) (4, 3)
C) (6, 1)
D) (7, 0)
E) (2, 5)

Çözüm:
İlk denklemi ikinci denklemle toplarsak:
2x = 10 ⇒ x = 5
Denklemde yerine koyduğumuzda y = 2 bulunur.
Doğru cevap: A) (5, 2)

Soru 4:
4x + y = 11 ve 3x – y = 4 denklemlerinin çözümü nedir?

A) (3, -1)
B) (2, 3)
C) (1, 7)
D) (0, 11)
E) (-1, 8)

Çözüm:
İki denklemi toplayarak 7x = 15 ve x = 3 bulunur. Denklemde yerine koyarak y = -1 elde edilir.
Doğru cevap: A) (3, -1)

Soru 5:
5x + 2y = 19 ve x – y = 2 denklemlerini çözünüz.

A) (1, -1)
B) (2, 3)
C) (3, -1)
D) (4, 1)
E) (0, 5)

Çözüm:
İkinci denklemi x = y + 2 olarak düzenleyip birinci denklemde yerine koyarsak:
5(y + 2) + 2y = 19
5y + 10 + 2y = 19
7y = 9 ve x = -1 bulunur.
Doğru cevap: A) (1, -1)

Soru 6:
x + 2y = 8 ve 3x – y = 7 sisteminin çözüm kümesi nedir?

A) (4, 2)
B) (3, 1)
C) (5, -2)
D) (2, 3)
E) (-1, 5)

Çözüm:
İlk denklemi x

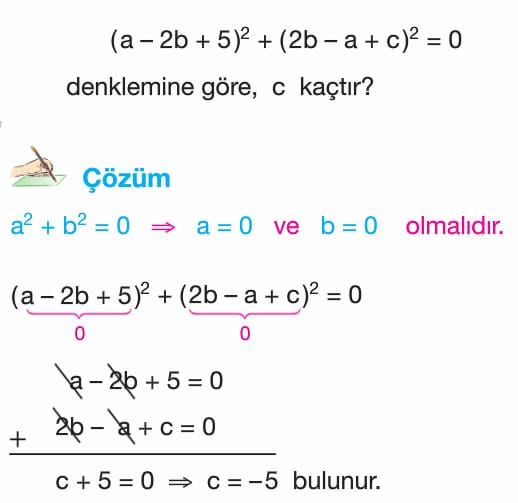
• ax + by + c = 0 denklemi bütün (x, y) gerçek sayı ikilileri için sağlanıyorsa a = b = c = 0 dır.
• a, b, c E R, a 0, b 0 olmak üzere, ax + by + c = 0 biçimindeki eşitliklere birinci dereceden iki bilinmeyenli denklemler denir.
• Birinci dereceden iki bilinmeyenli denklemler koordinat düzleminde bir doğru belirtir.

Soru: Bazı termometrelerin üzerinde, hava sıcaklıkları °C, bazılarında ise °F olarak verilir. Buradaki, °C dereceyi (SI birimine göre), °F ise fahrenheit dereceyi (Imperial birimine göre) ifade eder. Aslında bu hava sıcaklığının farklı iki birime göre ölçülmesidir. Bazı ülkelerin hava durumlarında °C, bazılarınınkinde °F kullanılır. Yukarıda °C ile °F arasındaki ilişkiyi gösteren grafik verilmiştir. Grafikte x ekseni °F ve y ekseni °C’yi göstermektedir. Örneğin, (32, 0) noktası 32°F nin O° ye karşılık geldiğini göstermektedir.

Yukarıdaki grafiğe göre 120°F yaklaşık kaç °C dir?
Grafikte 120°F den yukarı doğru bir çizgi çizildiğinde 120°F – 50° olduğu görülür.

Soru: x – 5y = 1 ve 2x + 3y = 15
denklem sisteminde x ve y değerini yerine koyma ile yöntemi ile bulalım.
ÇÖZÜM: 1. denklemden x i çekelim. x = 5y + 1
Bunu götürüp 2. denklemde x yerine koyalım.
2.(5y + 1) + 3y = 15   13y+2=15= y = 1 olur.
y = 1 için x = 5.1+1 = x = 6 bulunur.

Soru: x — y = 4 veya y = x — 4 doğrusunun grafiğini çizelim.
ÇÖZÜM: Bir doğrunun grafiğini çizmek için doğrunun geçtiği iki noktayı bulup bu noktaları birleştirmek yeterlidir.
x = 0 için y = —4 (0 , —4) noktasından geçer.
y = 0 için x = 4 (4 , 0) noktasından geçer.

Soru: y = x + 3 denkleminin grafiği ile Ox ve Oy eksenleri arasında kalan bölgede koordinatları tam sayı olan kaç nokta vardır? (Bölgenin sınır çizgileri üzerindeki noktalar dahildir.)
A) 10 B) 9 C) 8     D) 7     E) 6

Soru: Ardışık iki tam sayıdan biri y ise diğerinin alabileceği değerler toplamı 3x —1 ve ardışık iki tam sayıdan biri x  ise diğerinin alabileceği değerler toplamı y — 3 olduğuna göre, x + y kaçtır?
A) —8 B) —10 C) —12 D) —16 E) —18