Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler 9. Sınıf
Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler konu anlatımını bitirdikten sonra Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler Soru Çözümleri yazımıza bakmanızı tavsiye ederiz.
Sonraki Konu: Mutlak Değer İçeren Denklem ve Eşitsizlikler
Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler Ders Notu
Birinci Dereceden bir bilinmeyenli basit eşitsizlikler konusu 9. sınıf matematik müfredatında gerçek sayılar ve denklemler ünitesi içerisinde yer almaktadır. Bu yazımızda Birinci Dereceden bir bilinmeyenli eşitsizlikler konu anlatımı ve soru çözümleri videoları ile ders notlarını bulabilirsiniz. Konu içerisinde farklı öğretmenlere ait ders videoları paylaşılmıştır. Aynı konuyu farklı öğretmenlerden dinleyerek konuyu daha iyi pekiştirebilirsiniz.
Eşitsizlik Nedir?
Bir niceliğin diğer bir nicelikten büyük veya küçük olma durumunu belirten ifadelere ise eşitsizlik denir. Eşitsizliklerin ifade edilmesinde >, ≥, <, ≤ sembolleri kullanılır.
ax + b > 0 , ax + b ≥ 0 , ax + b < 0 , ax + b ≤ 0 şeklinde ifade edilebilen eşitsizliklere birinci dereceden bir bilinmeyenli eşitsizlikler denir.
2x – 3 > 5 , x – 2 < 0 , 25 – a ≤ 3a ifadeleri birinci dereceden bir bilinmeyenli eşitsizliklere birer örnektir. Denklemler ve eşitsizlikler, gerçek hayat durumlarının matematiksel olarak ifade edilmesinde ve incelenmesinde kullanılır.
Bir denklemde/eşitsizlikte değişkenin bazı değerleri eşitliği/eşitsizliği sağlayabilirken bazıları sağlamayabilir. Denklemi/eşitsizliği sağlayan sayıların kümesine o denklemin/eşitsizliğin çözüm kümesi denir.
Eşitsizliğin özellikleri
Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler Soru Çözümleri
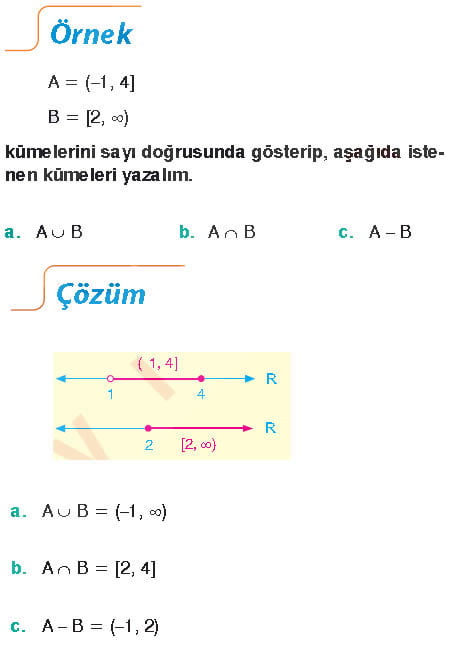
Gerçek Sayılarda Aralık Kavramı
1. Açık Aralık
2. Açık Aralık
3. Yarı açık aralık
Aralık Kavramı Çözümlü Örnekler
Çözümlü Örnek Test Soruları
Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler
Soru 1: 3x – 5 > 1 eşitsizliğini sağlayan en küçük tam sayı değeri nedir?
A) 1
B) 2
C) 3
D) 4
Cevap: C
Çözüm: 3x – 5 > 1 eşitsizliğini çözelim. 3x > 6 olur, her iki tarafı 3’e bölersek x > 2 elde edilir. En küçük tam sayı değeri 3’tür.
Soru 2: 4x + 7 ≤ 19 eşitsizliğinin çözüm kümesi nedir?
A) x ≤ 3
B) x < 2
C) x ≥ 4
D) x > 5
Cevap: A
Çözüm: 4x + 7 ≤ 19 eşitsizliğini çözersek, 4x ≤ 12 olur. Her iki tarafı 4’e böldüğümüzde x ≤ 3 elde edilir.
Soru 3: -2x + 6 < 10 eşitsizliğini sağlayan tam sayı değerleri nelerdir?
A) x ≤ -3
B) x > -1
C) x < 2
D) x ≥ 4
Cevap: C
Çözüm: -2x < 4 olur ve her iki tarafı -2’ye bölersek (işaret değişir) x > -2 elde edilir.
Soru 4: 5 – x ≥ 2 eşitsizliğinin çözümü nedir?
A) x ≥ 3
B) x ≤ 3
C) x ≥ -3
D) x < 5
Cevap: B
Çözüm: 5 – x ≥ 2 eşitsizliğinden -x ≥ -3 elde edilir. Her iki tarafı -1 ile çarparak x ≤ 3 sonucuna ulaşırız.
Soru 5: 3x – 7 < 2x + 5 eşitsizliğinin çözüm kümesi nedir?
A) x < 12
B) x > 5
C) x < 7
D) x ≥ 1
Cevap: A
Çözüm: Her iki taraftan 2x çıkarırsak, x < 12 elde edilir.
Soru 6: 4x + 3 > 2x + 11 eşitsizliğini sağlayan en küçük tam sayı değeri nedir?
A) 3
B) 4
C) 5
D) 6
Cevap: C
Çözüm: Eşitsizliği çözersek 2x > 8 ve x > 4 elde edilir. En küçük tam sayı değeri 5’tir.
Soru 7: -3x + 2 ≤ 5x – 6 eşitsizliğinin çözümü nedir?
A) x ≥ 2
B) x ≤ 1
C) x ≥ -2
D) x < -1
Cevap: B
Çözüm: Her iki tarafa 3x eklersek, 2 ≤ 8x – 6 olur. Çözüm x ≤ 1 olur.
Soru 8: x – 4 > 0 eşitsizliğinin çözüm kümesi nedir?
A) x > 4
B) x < 4
C) x ≤ 4
D) x = 4
Cevap: A
Çözüm: Eşitsizliği çözersek, x > 4 sonucuna ulaşırız.
Soru 9: 2x – 1 ≥ x + 3 eşitsizliğinin çözümü nedir?
A) x ≥ 4
B) x > 2
C) x ≤ -4
D) x ≥ 5
Cevap: A
Çözüm: Her iki taraftan x çıkarırsak, x ≥ 4 elde edilir.
Soru 10: 6 – 2x ≤ 8 eşitsizliğini sağlayan en büyük tam sayı değeri nedir?
A) 1
B) 0
C) -1
D) -2
Cevap: C
Çözüm: -2x ≤ 2 ve x ≥ -1 bulunur.
Örneğin, -2 < 5 iken -2 + 7 < 5 + 7 ise, 5 < 12 dir.
Örneğin, 2 < 8 iken 2 . 6 < 8 . 6 ise, 12 < 48 dir.
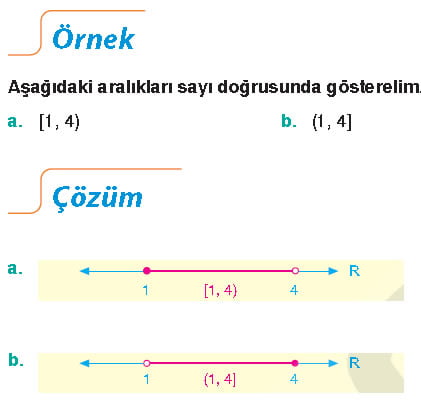
a < x < b şeklinde ifade edilen aralıklara açık aralık denir. Açık aralıklarda uç noktalar çözüm kümesine dahil değildir. a ≤ x ≤ b şeklinde ifade edilen aralıklara kapalı aralık denir. Kapalı aralıklarda uç noktalar çözüm kümesine dahildir. Örneğin, Aşağıda verilen aralıkları sayı doğrusunda gösterin.
Bir eşitsizlikteki ifadelerin işareti değişirse eşitsizliğin yönü değişir. Bir eşitsizliğin her iki tarafına aynı sayı eklenir ya da çıkarılırsa eşitsizliğin yönü değişmez. Bir eşitsizliğin her iki tarafı pozitif bir sayı ile çarpılır ya da bölünürse, eşitsizliğin yönü değişmez.
Aynı yönlü iki ya da daha fazla eşitsizlik sadece taraf tarafa toplanabilir. Çıkarılamaz, çarpılamaz ya da bölünemez.
Birinci dereceden iki bilinmeyenli bir eşitsizlik sistemini sağlayan noktalar kümesi analitik düzlemde her iki eşitsizliği de sağlayan ortak noktalardan oluşan taralı bir bölgeyi ifade eder.
El Harezmi: Ebu Ca’fer Muhammed bin Musa el-Hârezmî İslam dünyasında cebir ilminin kurucusu kabul edilen matematikçi, astronom ve coğrafyacıdır. Hârezmî’nin yazdığı “El’ Kitab’ül-Muhtasar fi Hisab ‘il Cebri ve’l Mukabele’’ (Cebir ve Eşitlik Üzerine Özet Kitap) düzenli biçimde telif edilmiş, adında “cebir” kelimesini taşıyan ilk matematik kitabıdır. Kitabında cebirsel denklemleri çözerken analitik çözüm yanında geometrik çizimi de kullanan ilk matematikçidir. Ayrıca eserinde sayılar dâhil hiçbir aritmetiksel ve cebirsel işlem için sembol kullanmamış ve bütün işlemleri sözel olarak ifade etmiştir. Hârezmî, ilk defa birinci ve ikinci dereceden denklemleri analitik metotlarla bir bilinmeyenli denklemleri de cebirsel ve geometrik metotlarla çözmenin kurallarını ve usullerini tespit etmiştir. Matematikte ilk defa sıfır rakamını kullanmıştır. Kendi adıyla anılan “algoritma” yı ortaya çıkarmış ve bugün Arap rakamları olarak da bilinen Hint numaralama sistemini tanıtmıştır. Kesirlerde, işlemler de içinde olmak üzere birçok aritmetik yöntem geliştirmiştir. Hârezmî’nin bu çalışmaları, evrenin ahengini matematik yoluyla anlamaya çalışanlara yüzyıllar boyunca ilham vermiştir.

































Oldukça kolay bir konu. Keşke matematik hep böyle kolay olsa ne güzel olurdu. Hocamızın ağzına sağlık.