Bu yazımızda, 9. sınıf matematik müfredatında Dik Üçgen ve Trigonometri konusunda yer alan Birim Çember ders notları yer almaktadır. Konuyu bitirdikten sonra alttaki linke tıklayarak çözümlü sorular ve testlere de bakabilirsiniz.
Birim Çember Çözümlü Sorular ve Testler
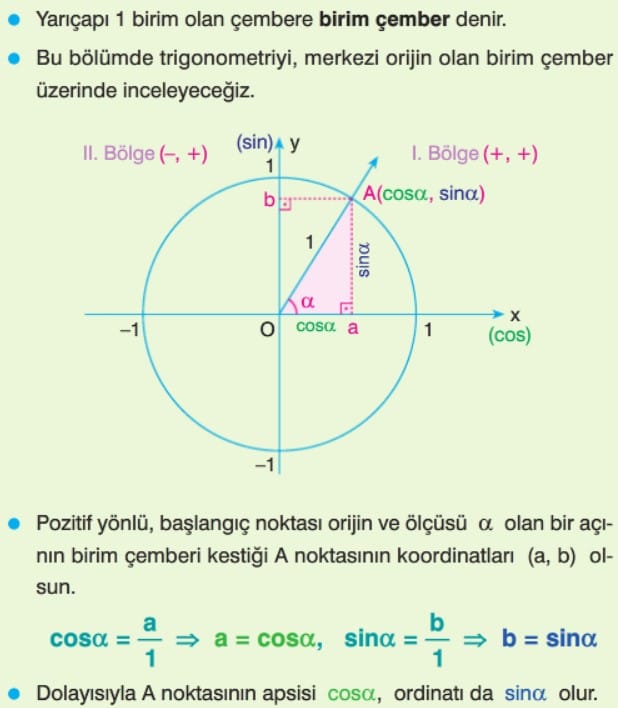
Merkezi 0(0, O) (orijin) ve yarıçapı 1 birim olan çembere birim çember denir.
Birim çemberde, köşe noktası orijinde ve başlangıç kenarı pozitif x ekseni olan açılar standart konumdadır. Aşağıdaki birim çemberde,
açısı standart konumdadır.
Buna göre, P(cos α, sin α) olur.
P noktasının apsisi cosα ya, ordinatı sinα ya eşittir.
x ekseni kosinüs ekseni, y ekseni ise sinüs ekseni diye adlandırılır.
Birim çemberde, x = 1 doğrusu tanjant ekseni, y = 1 doğrusu kotanjant ekseni diye adlandırılır.
O° ile 90° arasında α arttıkça; sinα ve tanα nın değeri artar, cosα ve cotα nın değeri azalır.
Örnek: sin70°, cos70° ve tan70° değerlerini küçükten büyüğe doğru sıralayalım.
Çözüm: cos70° = sin 20° ve sin 20° < sin 70° dir.
sinüs ve kosinüs fonksiyonlarının alabileceği en büyük değer 1 dir. Ancak tan 70° > 1 dir. Çünkü tan 45° = 1 dir ve birim çembere bakılırsa 90° ye kadar tanjant sürekli artar.
Sonuç olarak; cos 70° < sin 70° < tan 70° bulunur.
90° ile 180° arasındaki açıların kosinüs, tanjant ve kotanjant değerleri negatiftir.
Birim çember, matematikte trigonometrik fonksiyonların grafiksel olarak temsil edildiği bir dairedir. Birim çember, yarıçap uzunluğunun 1 birim olduğu bir daireyi ifade eder. Genellikle, (0,0) noktası merkezde olmak üzere, çember üzerinde birim uzunluğundaki yarıçapa sahip dairenin grafiği olarak düşünülür.