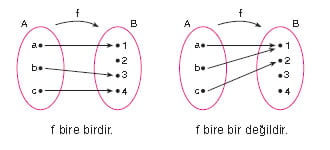
Bire bir fonksiyon nedir?
Boş olmayan A ve B kümeleri için f : A → B fonksiyonunun tanım kümesindeki her farklı elemanın görüntüsü farklı ise, f fonksiyonuna bire bir fonksiyon denir.
∀a, b ∈ A için, a ≠ b ⇒ f(a) ≠ f(b) ya da f(a) = f(b) ⇒ a = b koşulu sağlanıyorsa f fonksiyonu bire birdir.
Çözümlü Test Soruları
Soru 1:
f: R → R, f(x) = 2x + 3 fonksiyonu bire bir midir?
Çözüm:
- f(x₁) = f(x₂) diyelim:
2x₁ + 3 = 2x₂ + 3 ⇒ 2x₁ = 2x₂ ⇒ x₁ = x₂ - Sonuç: Bire birdir. (Doğrusal fonksiyonlar eğimi sıfır değilse bire birdir).
Soru 2:
f: R → R, f(x) = x² + 1 fonksiyonu bire bir midir?
Çözüm:
- f(2) = 5 ve f(-2) = 5 (farklı x’ler aynı çıktıyı verir).
- Sonuç: Bire bir değildir. (Çünkü x ≠ -x iken f(x) = f(-x)).
Soru 3:
f: N → N, f(x) = x + 5 fonksiyonu için aşağıdakilerden hangisi doğrudur?
A) Örten fonksiyondur
B) Bire bir fonksiyondur
C) Sabit fonksiyondur
D) Hiçbiri
Çözüm:
- f(x₁) = f(x₂) ⇒ x₁ + 5 = x₂ + 5 ⇒ x₁ = x₂
- Sonuç: Bire birdir (B).
- Ayrıca, örten değildir (örneğin 1 ∈ N’in ön görüntüsü yoktur).
Soru 4:
Aşağıdaki fonksiyonlardan hangisi bire bir değildir?
A) f(x) = 3x – 7
B) f(x) = eˣ
C) f(x) = |x|
D) f(x) = 1/x (x ≠ 0)
Çözüm:
- C seçeneği: f(2) = 2 ve f(-2) = 2 → Bire bir değil.
- Diğerleri bire birdir (A: doğrusal, B: üstel, D: ters orantı).
Soru 5:
f: A → B fonksiyonu bire bir ve A = {1, 2, 3} ise, aşağıdaki görüntü kümelerinden hangisi olası değildir?
A) B = {4, 5, 6}
B) B = {0, 1}
C) B = {10, 20, 30}
D) B = {π, e, √2}
Çözüm:
- Bire bir fonksiyon için B’nin eleman sayısı ≥ A’nın eleman sayısı olmalıdır.
- B seçeneği: 2 eleman < 3 eleman → Bire bir olamaz.
- Cevap: B
Kısa Bilgiler
✓ Bire bir fonksiyonların tersi vardır.
✓ Sabit fonksiyonlar (f(x) = c) bire bir değildir.
✓ f(x) = ax + b (a ≠ 0) her zaman bire birdir.