Bernoulli İlkesi, sıvı ve gazların akışı sırasında basınç, hız ve potansiyel enerjileri arasındaki ilişkiyi açıklayan bir prensiptir. 9. sınıf fizik müfredatında Bernoulli İlkesi, akışkanlar mekaniği konusunun temelini oluşturur ve sıvıların davranışlarını anlamada önemli bir rol oynar.

Bernoulli İlkesi

Sıvılar ve gazlar, hareket edebilen akışkan maddelerdir. Hareket halindeki bu maddelerin meydana getirdiği basınca “akışkan basıncı” denir. Akışkanlar, bir noktadan başka bir noktaya basınç farkı sebebiyle hareket ederler. İki nokta arasındaki basınç farkı ne kadar büyükse, akışkanın o noktalar arasındaki hareketi de o kadar hızlı olur.

İsviçreli bilim insanı Daniel Bernoulli, akışkanların hızlı aktığı yerde, basıncın düştüğünü kendi adıyla bilinen ilke ile açıklamıştır. Bernoulli ilkesi, akışkanların (sıvı ve gaz) düzgün akması, sıkışmaz olması durumunda geçerlidir.

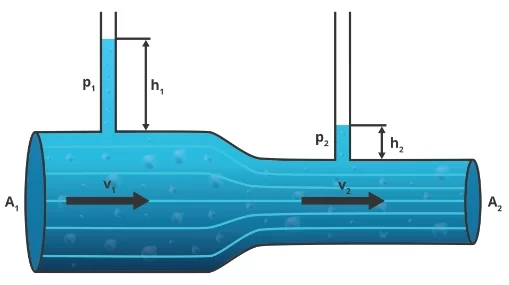
• Borunun kesiti azaldıkça akışkanın hızı artar. Buna karşılık akışkanın boruya uyguladığı basınç azalır.V₂>V₁​ ve P₁>P₂​ olur.Borulardaki su yükseklikleri arasında:

  h₁>h₂ olur.

Bernoulli İlkesinin Günlük Yaşamdaki Etkileri

• Rüzgârlı havalarda şemsiyenin ters dönmesi de basıncın bir sonucudur. Şemsiyenin geometrik şeklinden dolayı şemsiyenin üzerinden geçen hava hızlanır ve havanın basıncı düşer. Şemsiyenin alt kısmındaki basınç, üstüne göre daha fazla olduğundan şemsiye ters döner.
• Yarış otomobillerin arka kısmında, uçaklardakinden ters bir yapıya sahip olan kanatlar bulunur. Bu kanatlar, yüksek hızda hareket eden yarış otomobillerinin uçmasını önler ve otomobili yola daha iyi kavramasını sağlar.
• Bahçeyi hortumla sularken hortumun ucunu elimizle sıkarak suyun daha hızlı aktığını görürüz. Bunun sebebi, kesit alanı azaltıldığında akışkanın hızının artmasıdır.
• Bir musluğun ağzından damlayan su damlaları aşağı doğru düşerken hızlanır ve küçülür. Bunun nedeni akışkanların hızlandıkça kesit alanlarının azalmasıdır.
• Hareket halindeki bir tren yanından bir araç geçerken araçlar arasındaki havanın hızı artar. Araçlar arasındaki basınç azaldığından araçlar içe doğru itilir.
• Aynı durum hızlı hareket eden bir aracın yanından geçtiğimizde bize bir kuvvet uygulayarak aracı bize doğru çekmesinde de geçerlidir. Metro istasyonlarında bu basınç farkından korunmak için güvenlik bantları çekmek önemlidir.
• Kalbin kasılıp gevşemesi sırasında kanın atardamara duvarına yaptığı basınca tansiyon denir. Kanın kasılması sırasında kanın atardamara duvarına yaptığı basınca büyük tansiyon, kanın kasılmasının ardından kanın atardamardan duvara yaptığı basınca ise küçük tansiyon denir.
• Hızlı hareket eden bir arabanın camı hafif aralandığında içerideki durağan hava dışarı doğru çekilir ve dış hava basıncı kaynaklı içeriye doğru bir basınç farkı oluşur.
• Rüzgârlı havalarda havanın sürati arttığı için dış alan sibopslarının yerleştirildiği bölgedeki basınç düşer. Basınç düştüğünde ise basınç farkı nedeniyle tekerlek içerisindeki hava dışarı kaçar ve siboplar gevşer.
• Bir flüt veya bir başka üflemeli çalgıyı kullanırken çaldığımızda havanın hızlanıp dar bir alanda ilerleyerek ses çıkarmasının sebebi basınç farkıdır. Bu basınç farkı çalgının daha iyi ses çıkarmasını sağlar.

Özet:

Bernoulli İlkesi Nedir?

Bernoulli İlkesi, bir akışkanın hızı arttığında, basıncının azaldığını; hızı azaldığında ise basıncının arttığını ifade eder. Bu ilke, enerji korunumu prensibine dayanır. Bernoulli İlkesi şu şekilde özetlenebilir:

• Bir akışkanın hızı arttıkça, basıncı azalır.
• Bir akışkanın hızı azaldıkça, basıncı artar.

Bu ilke, hem sıvılar hem de gazlar için geçerlidir.

Bernoulli Denklemi

Bernoulli İlkesi’nin matematiksel ifadesi şu şekildedir:

P + (1/2) * d * v² + d * g * h = sabit

• P: Basınç (Pascal)
• d: Akışkanın yoğunluğu (kg/m³)
• v: Akışkanın hızı (m/s)
• g: Yer çekimi ivmesi (9.8 m/s²)
• h: Akışkanın yüksekliği (metre)

Bu denklem, akışkanın basıncı, hızı ve potansiyel enerjisi arasında bir denge olduğunu ifade eder. Enerji korunumu gereği, bir faktör artarsa diğerleri azalmalıdır.

Bernoulli İlkesi’nin Uygulama Alanları

1. Uçak Kanatları
   • Uçak kanatlarının üst kısmı kavisli, alt kısmı ise düzdür. Hava, kanadın üst kısmında daha hızlı hareket eder, bu da basıncın düşmesine neden olur. Alt kısımdaki hava ise daha yavaş hareket eder, bu yüzden daha yüksek bir basınç uygular. Üstte düşük, altta yüksek basınç farkı oluşur ve uçak bu sayede havalanır.
2. Karbonatör ve Spreyler
   • Sprey ve parfüm şişelerinde, sıvı bir bölmeden dar bir boru aracılığıyla dışarıya püskürtülür. Hızla geçen hava, sıvının üstündeki basıncı düşürür ve sıvı yukarı çekilir. Bu da Bernoulli İlkesi’ne dayanan bir uygulamadır.
3. Venturi Borusu
   • Daralan borularda akışkanın hızı artar, basıncı düşer. Venturi boruları, bu prensipten faydalanarak sıvı ve gaz akışlarını ölçmek için kullanılır.
4. Rüzgar Türbinleri
   • Rüzgar türbinlerinin kanatlarına hızla çarpan hava, kanatların bir yüzeyinde daha düşük basınç yaratır. Basınç farkı sayesinde kanatlar döner ve enerji üretilir.

Örnek Sorular

1. Bir su borusunda suyun akış hızı daralan bir bölgede artıyor. Bu durumda basınç nasıl değişir?
   • Çözüm: Akışkanın hızı arttıkça basınç düşer. Bu yüzden daralan bölgede basınç azalır.
2. Bir uçak havalanırken kanadın altındaki basınç mı yoksa üstündeki basınç mı daha büyüktür?
   • Çözüm: Kanadın altındaki basınç daha büyüktür, çünkü üst kısımdaki hava daha hızlı hareket ettiği için basınç düşmüştür.