BELİRLİ İNTEGRAL VE ÖZELLİKLERİ

PARÇALI FONKSİYONUN İNTEGRALİ

MUTLAK DEĞER FONKSİYONUNUN İNTEGRALİ

Çözümlü Örnek Test Soruları

Soru 1: Temel Belirli İntegral Hesaplama
∫(1’den 3’e) (2x + 4) dx ifadesinin değeri kaçtır?

Çözüm:
Önce integralin genel ifadesini bulalım:
∫(2x + 4) dx = x² + 4x + C

Belirli integrali hesaplayalım:
[x² + 4x](1’den 3’e) = (3² + 4·3) – (1² + 4·1)
= (9 + 12) – (1 + 4)
= 21 – 5 = 16

Cevap: 16

---

Soru 2: Polinom Fonksiyonunun İntegrali
∫(0’dan 2’ye) (3x² – 2x + 1) dx integralinin sonucu kaçtır?

Çözüm:
Genel integrali alalım:
∫(3x² – 2x + 1) dx = x³ – x² + x + C

Belirli integrali hesaplayalım:
[x³ – x² + x](0’dan 2’ye) = (8 – 4 + 2) – (0 – 0 + 0)
= 6 – 0 = 6

Cevap: 6

---

Soru 3: Köklü Fonksiyon İntegrali
∫(1’den 4’e) √x dx ifadesinin değeri nedir?

Çözüm:
√x = x^(1/2) şeklinde yazıp integral alalım:
∫x^(1/2) dx = (2/3)x^(3/2) + C

Belirli integrali hesaplayalım:
[(2/3)x^(3/2)](1’den 4’e) = (2/3)·8 – (2/3)·1
= 16/3 – 2/3 = 14/3

Cevap: 14/3

---

Soru 4: Mutlak Değer Fonksiyonu İntegrali
∫(-2’den 3’e) |x| dx integralinin değeri kaçtır?

Çözüm:
Mutlak değeri parçalı şekilde yazalım:
∫(-2’den 0’a) (-x) dx + ∫(0’dan 3’e) x dx
= [-x²/2](-2’den 0’a) + [x²/2](0’dan 3’e)
= (0 – (-2)) + (9/2 – 0)
= 2 + 4.5 = 6.5

Cevap: 13/2 (veya 6.5)

---

Soru 5: Trigonometrik Fonksiyon İntegrali
∫(0’dan π/2’ye) sinx dx integralinin sonucu nedir?

Çözüm:
∫sinx dx = -cosx + C

Belirli integrali hesaplayalım:
[-cosx](0’dan π/2’ye) = (-cos(π/2)) – (-cos0)
= (0) – (-1) = 1

Cevap: 1

---

Soru 6: Üstel Fonksiyon İntegrali
∫(0’dan 1’e) e^(2x) dx integralinin değeri kaçtır?

Çözüm:
∫e^(2x) dx = (1/2)e^(2x) + C

Belirli integrali hesaplayalım:
[(1/2)e^(2x)](0’dan 1’e) = (1/2)e² – (1/2)e⁰
= (1/2)(e² – 1)

Cevap: (e² – 1)/2

---

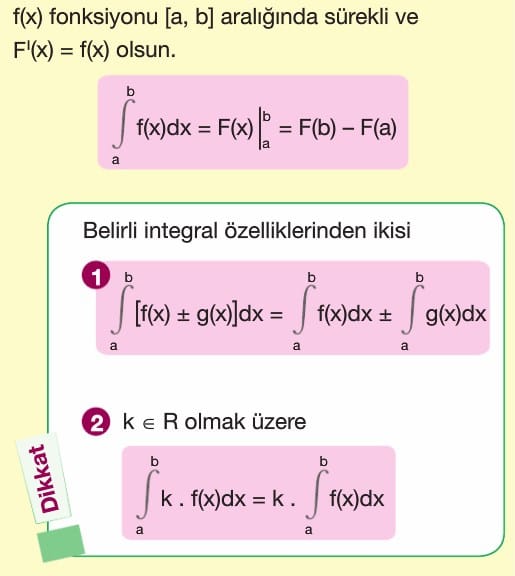
f(x) fonksiyonu [a,b] kapalı aralığında sürekli ve F'(x) = f(x) olsun. a dan b ye integral f(x) dx = F(x) a dan b ye = F(a) – F(b) dir.
Toplama ve Çıkarma durumundaki iki fonksiyonun belirli integrali ayrı ayrı hesaplanabilir.
Belirsiz integralde olduğu gibi belirli integralde de sabit çarpan integral dışına çıkabilir.
a dan a ya belirli integral ifadesinin sonucu sıfırdır. Fonksiyonun bir önemi yoktur.
a dan b ye belirli integralinde sınırlar yer değiştirilirse sonuç işaret değiştirir.
a dan b ye belirli integralini, n sayısı a ile b arasında olmak üzere a dan n ye belirli integral + n den a ya belirli integral şeklinde parçalayabiliriz.
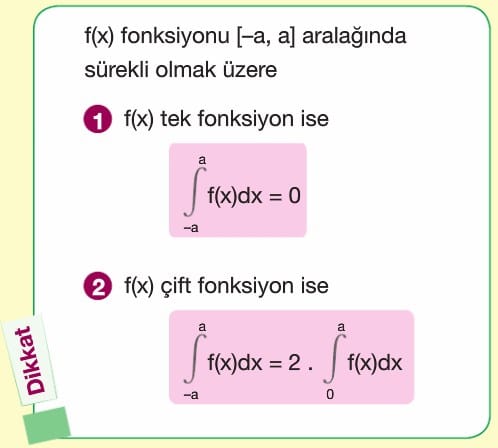
-a dan a ya belirli integrali, f tek fonksiyon ise sıfıra, çift fonksiyon ise 0 dan a ya integral f(x) in 2 katına eşittir.

Çıkmış Soru: Bir f fonksiyonunun grafiğinin x = a noktasındaki teğetinin eğimi 1, x=b noktasındaki teğetinin eğimi kök 3 tür. f”(x) ikinci türev fonksiyonu [a,b] aralığında sürekli olduğuna göre b den a ya integral f'(x).f”(x)dx integralinin değerini bulunuz.
Çözüm: a ve b sınırları yerine kök 3 ve bir yazıp, değişken değiştirme uygulandığında integralimiz u2/2 kök 3 den 1 e olur. İşlemi yaparsak sonuç -1 bulunur.

Soru: u(t) fonksiyonu bir dairenin tükettiği su miktarının kaç ton olduğunu göstermektedir. u'(t) = 3t2+18t fonksiyonu ise tüketilen su miktarının t aydaki artış hızını göstermektedir. Buna göre şebekeye ilk su verildikten sonraki geçen 4 ayda bu dairede kaç ton su tüketilmiştir.
Çözüm: u(t) fonksiyonu 3t2+18t ifadesinin integraline eşittir. Buradan sorunun cevabı 0 dan 4 e integral 3t2+18t ifadesi ile bulunabilir. İşlemleri yaparsak sonuç 100 ton bulunur.