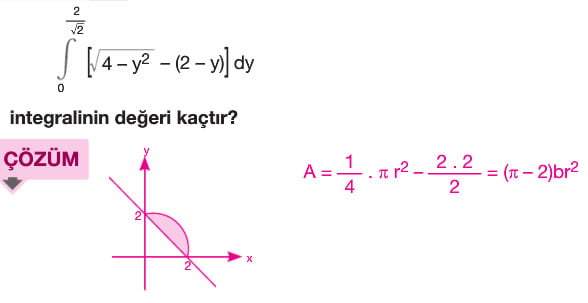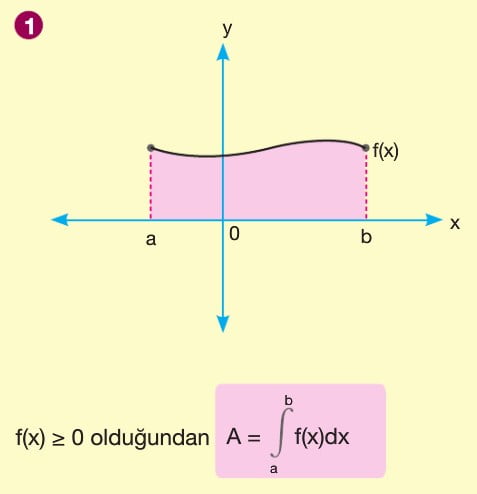
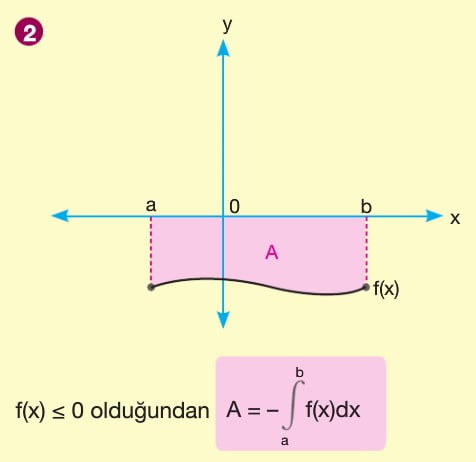
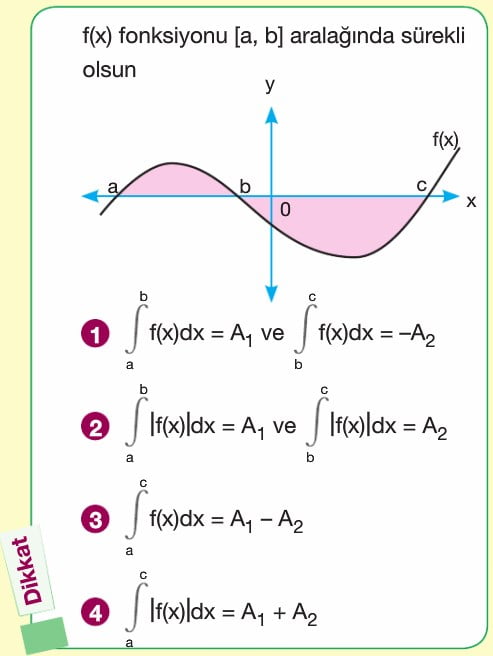
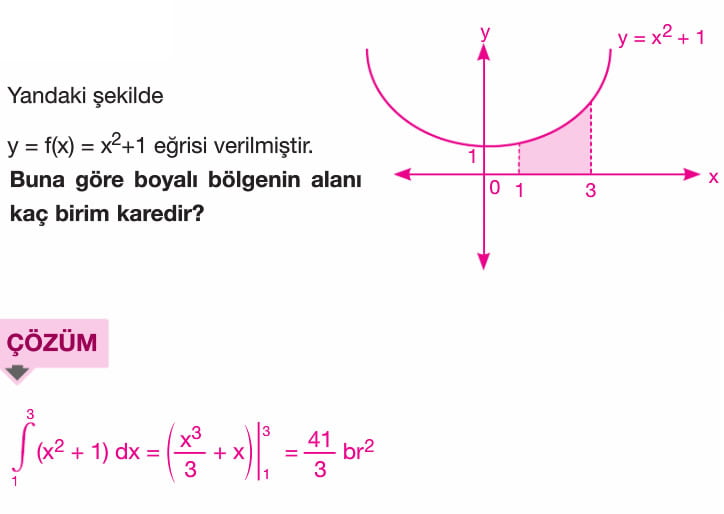
Belirli İntegral Alan Hesabı konu anlatımı soruları çözümleri Riemann Toplamı 12. Sınıf Ayt

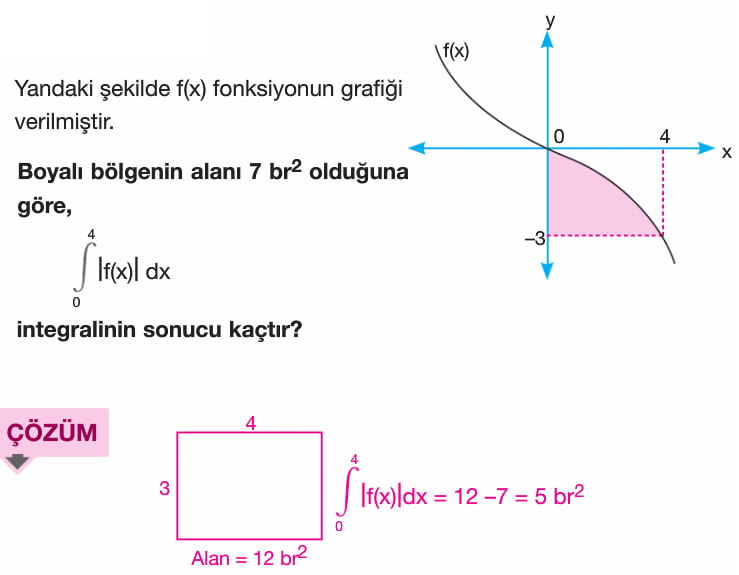
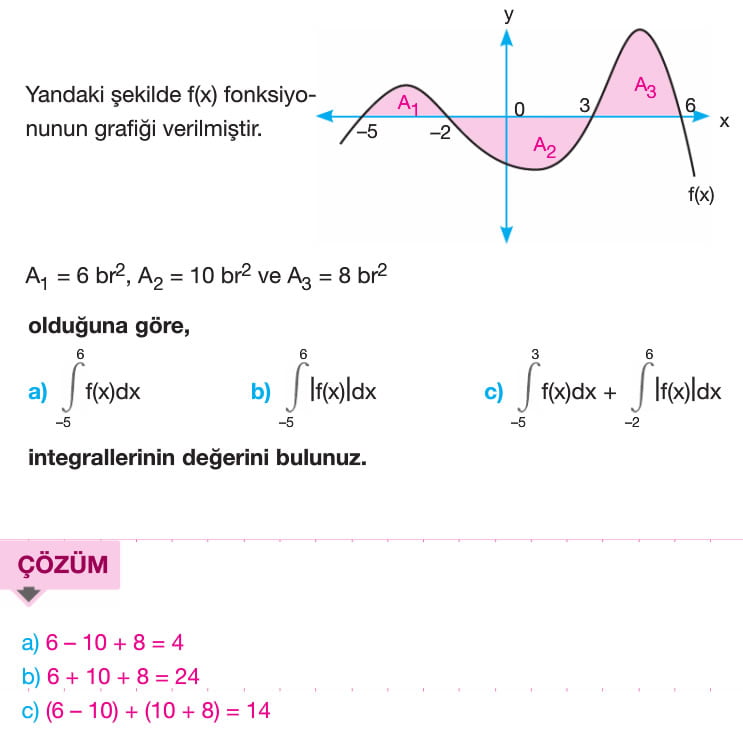
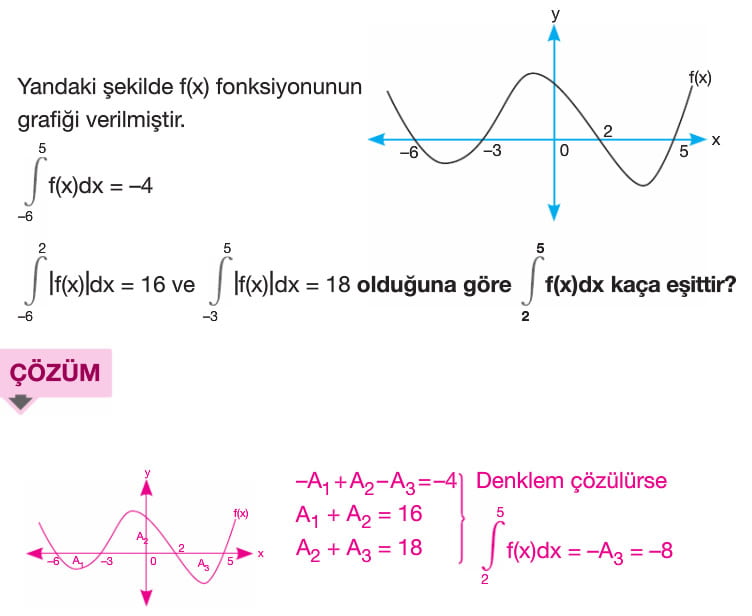
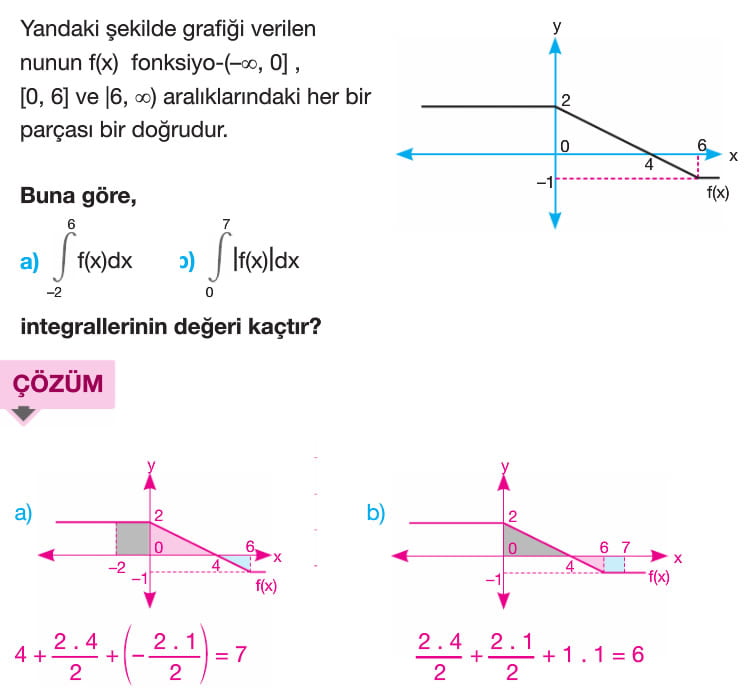
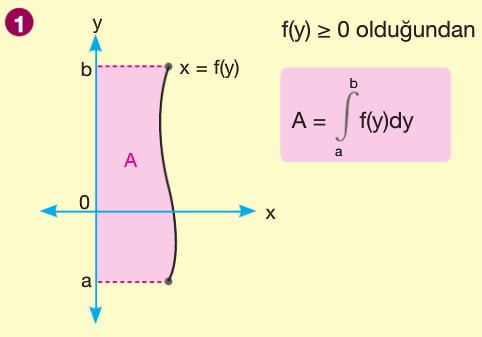
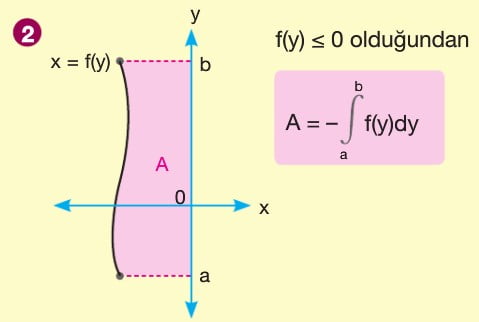
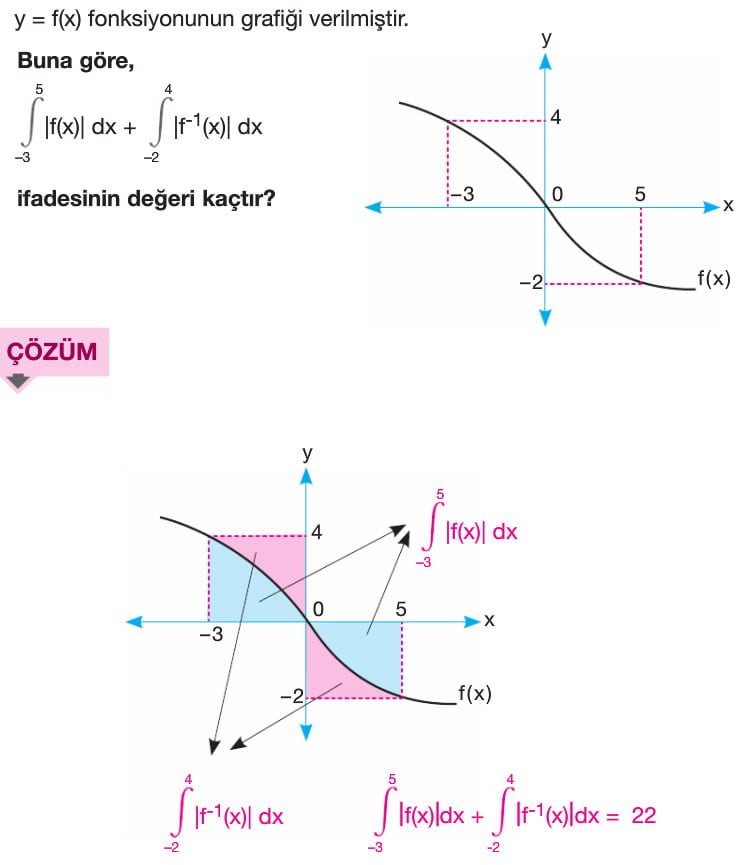
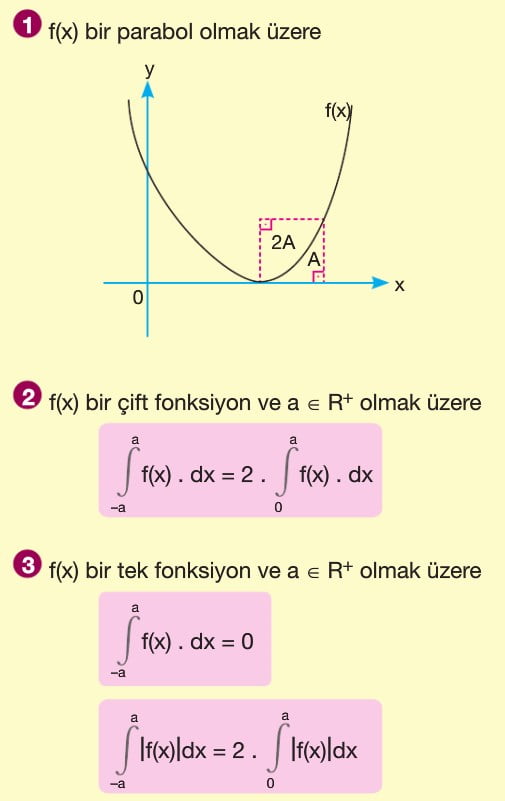
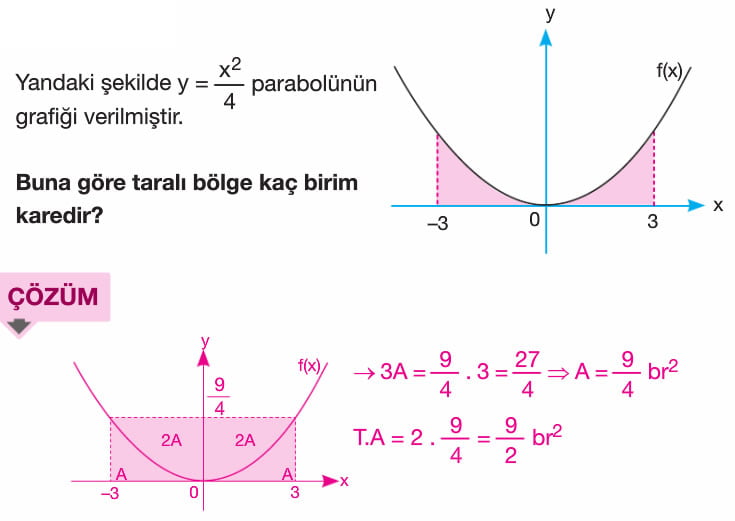
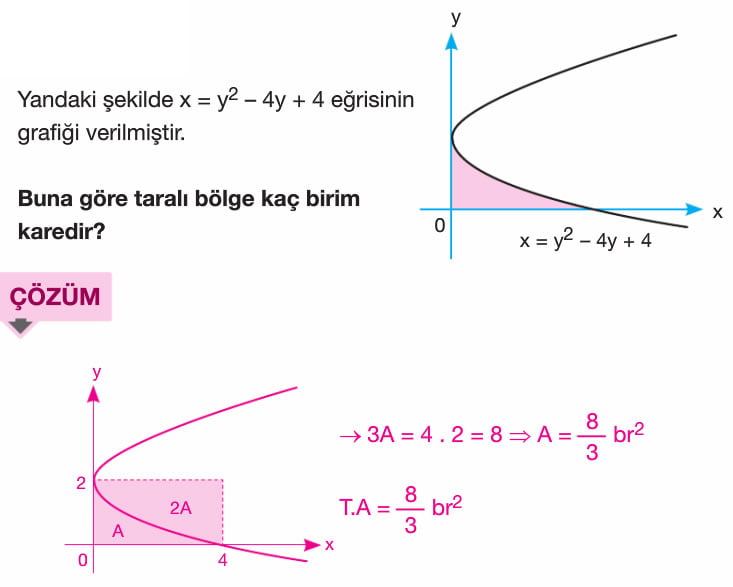
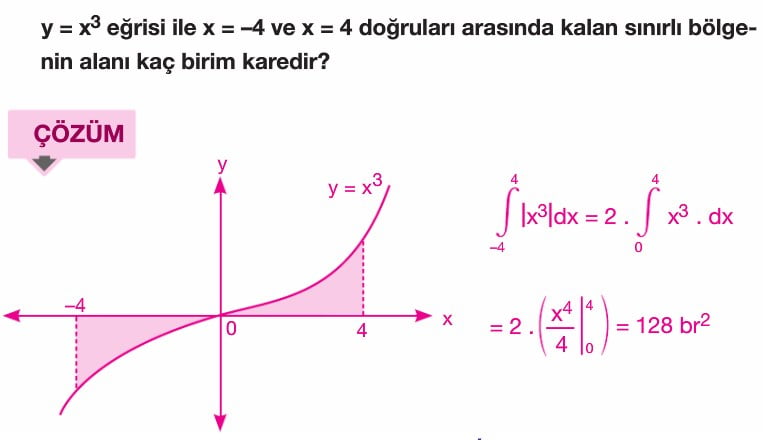
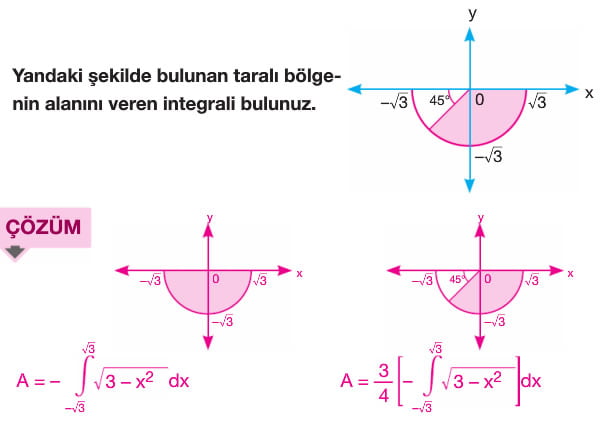
f(x) fonksiyonu [a,b] kapalı aralığında sürekli olmak üzere f(x) fonksiyonu ile x ekseni arasındaki alan A olsun. A = a dan b ye integral mutlak değer f(x) ile bulunur. x ekseninin üzerindeki alan a da n b ye integral f(x) e, x ekseninin altında kalan alan ise -(a dan b yeintegral f(x)) şeklindedir. Yani x ekseninin altında kalan alan bulunurken çıkan sonucun ters işaretlisi alınır.

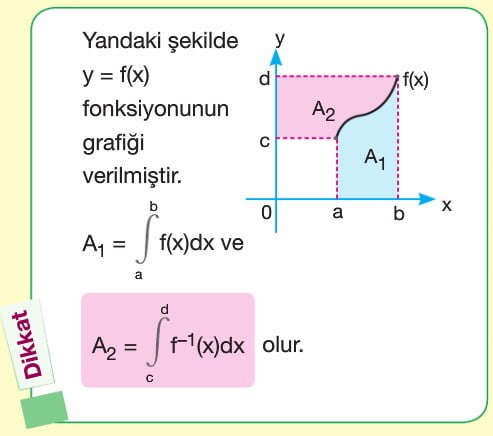
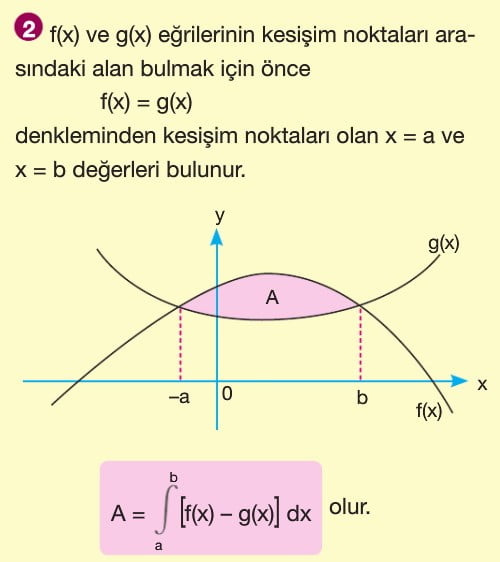
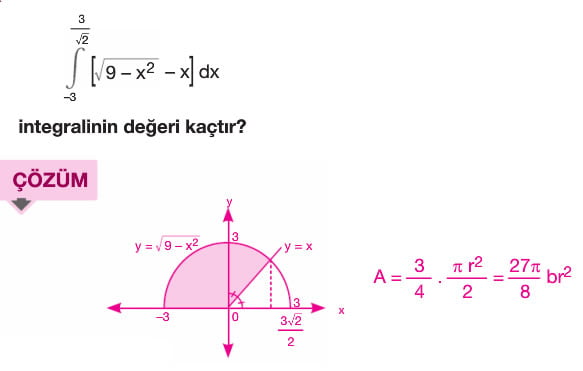
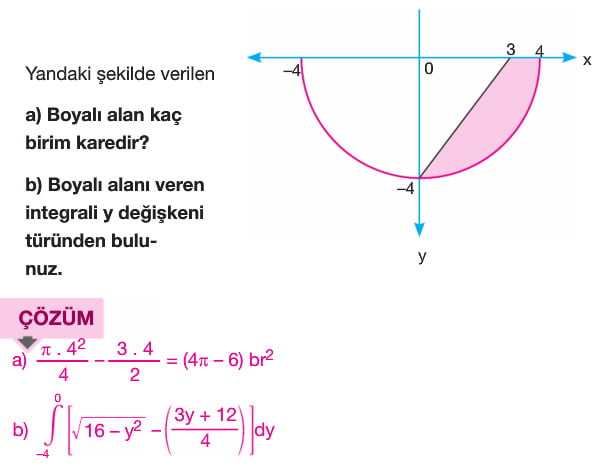
f(x) ve g(x) eğrileri ile x=a ve x=b doğruları tarafından sınırlandırılan bölgenin alanı A olsun. A = a dan b ye integral f(x)-g(x) (f(x) > g(x) olduğundan)
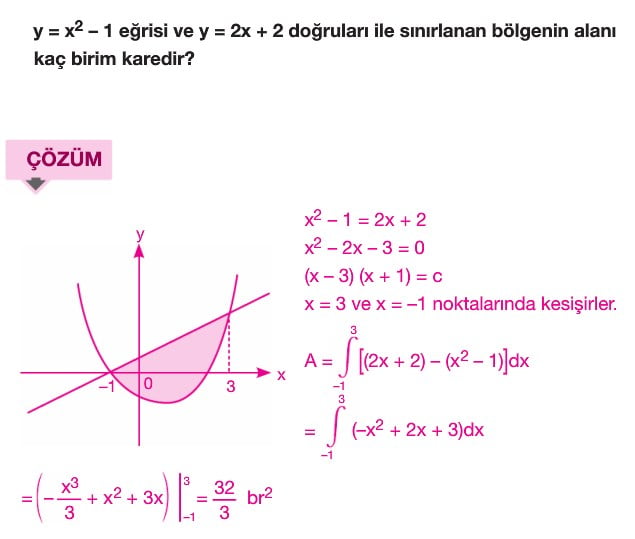
f(x) ve g(x) eğrilerinin kesişim noktaları arasındaki alanı bulmak için öncelikle f(x) = g(x) denkleminin çözümü yapılarak denklemlerin kesişim noktaları olan a ve b değerleri bulunur. Buradan A değeri a dan b ye integral f(x) - g(x) bağıntısı ile bulunur.
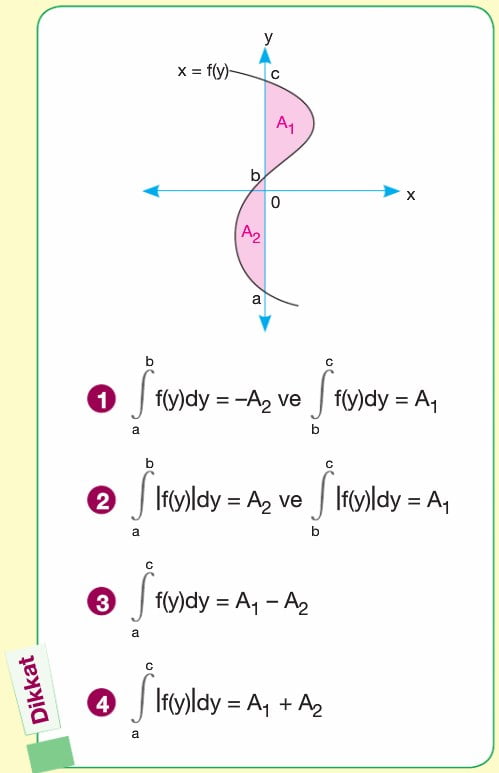
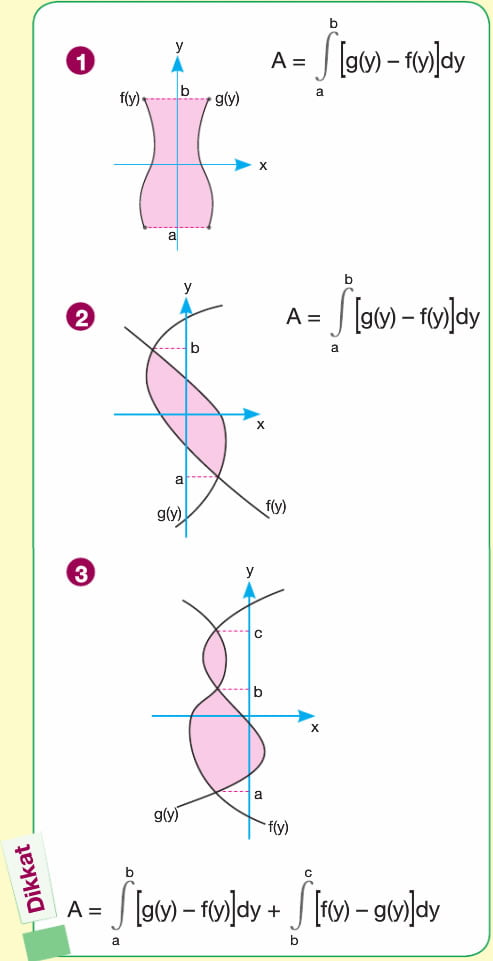
f(x) ve g(x) eğrilerinin ikiden fazla kesişim noktası var ve bu noktalar a, b, c olsunlar. Buradan A1 + A2 ifadesi a dan b ye integral f(x)-g(x) + b den c ye integral g(x) - f(x) bağıntısı ile bulunur.

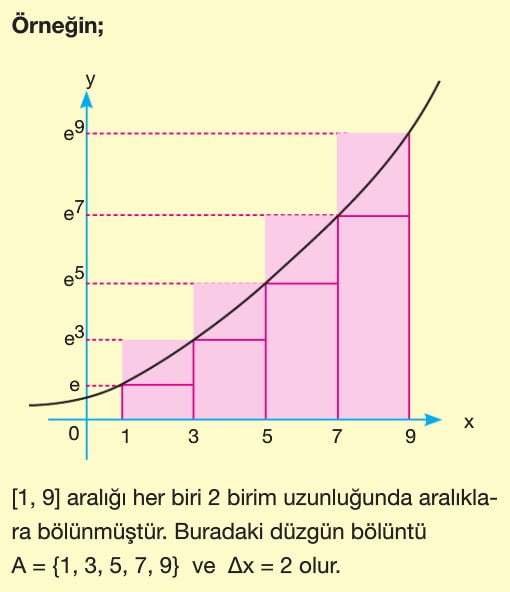
[a, b] kapalı aralığı
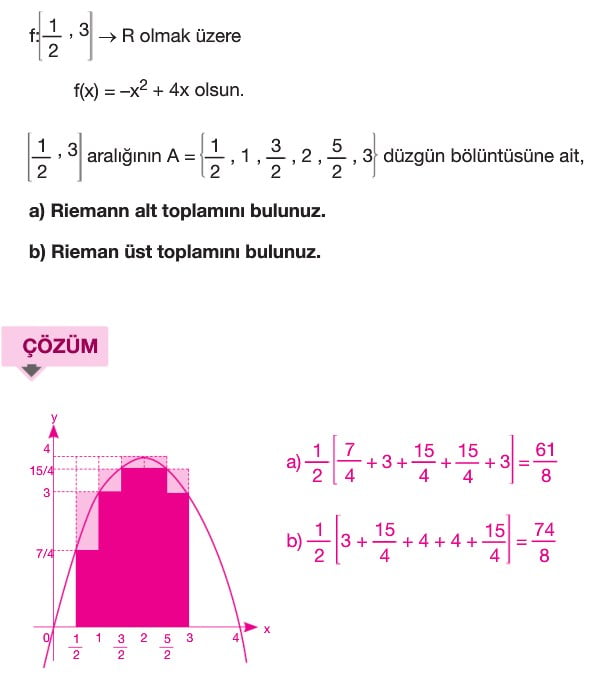
a = x0 ve b = xn olacak şekilde, [X0, X1] , [X1, X2] , , [xn _1 ,xn] şeklinde aralıklara bölündüğünde, A= (X0 , X1 , xn) kümesine [a, b] aralığının bir bölüntüsü denir. Bu n parçaya ayrılmış aralıklar eşit uzunlukta ise A bölüntüsüne düzgün bölüntü denir. Bu düzgün bölüntüdeki kapalı aralıkların her birinin uzunluğu Ax olsun. f fonksiyonu [a, b] aralığında pozitif tanımlı ve sürekli bir fonksiyon olsun. k elemanıdır {1,2,3,n} olmak üzere f(x) fonksiyonunun [xk _ 1 , xk] aralığındaki
En küçük değeri fk
En büyük değeri Fk
Herhangi bir değeri fî
olsun.