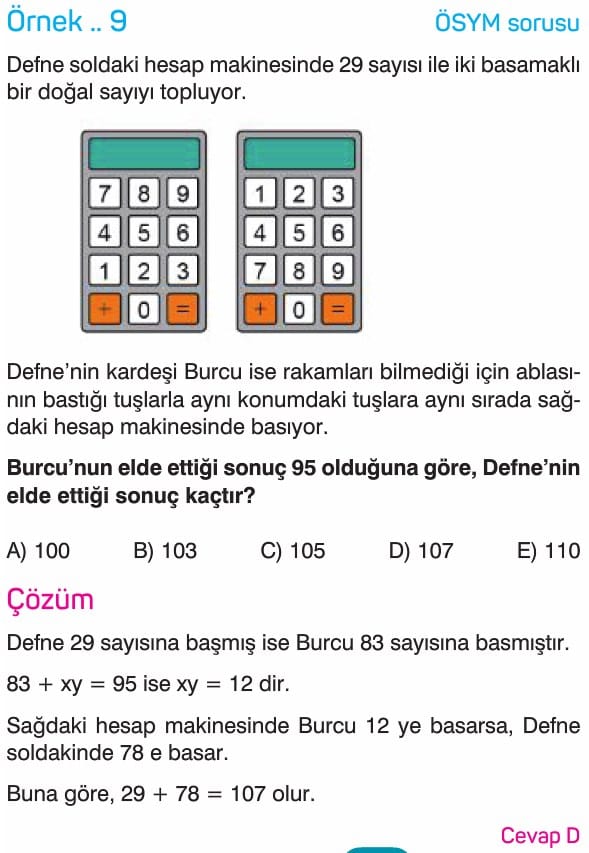
Basamak Kavramı Tyt

Sayfanın sonunda Basamak Kavramı ders videoları bulunmaktadır.

BASAMAK

Bir doğal sayıyı oluşturan her bir rakama bu sayının basamağı denir.

Örnek:
7 bir basamaklı
29 iki basamaklı
453 üç basamaklı
7843 dört basamaklı birer sayıdır.

Bilgi: A, B, C ve D birer rakam olmak üzere,
AB iki basamaklı sayı,
ABC üç basamaklı sayı,
ABCD dört basamaklı sayı olarak alınır.
ABC üç basamaklı sayısında;
Birler basamağındaki rakam C dir.
Onlar basamağındaki rakam B dir.
Yüzler basamağındaki rakam A dır.

Örnek: 79 iki basamaklı bir sayıdır.
Bu sayının birler basamağındaki rakam 9, onlar basamağındaki rakam 7 dir.

Örnek:  468 üç basamaklı sayısında; birler basamağındaki rakam B, onlar basamağındaki rakam 6 ve yüzler basamağındaki rakam 4 tür.

DOĞAL SAYILARIN ÇÖZÜMLENMESİ

Bilgi: AB iki basamaklı, ABC üç basamaklı ve ABCD dört basamaklı sayılarının çözümlenmiş biçimi:
AB = 10.A + B
ABC = 100.A + 10.B + C
ABCD = 1000.A + 100.B + 10.C + D olur.

İki basamaklı AB sayısının onlar basamağındaki rakam 0 olamaz. Aynı şekilde, üç basamaklı ABC sayının yüzler basamağındaki rakam 0 olamaz.

AB ifadesi aksi belirtilmedikçe A . B biçiminde anlaşılmalıdır.
“AB iki basamaklı sayıdır” biçiminde verilirse,
AB = 10.A + B anlamına gelir.

Bilgi: ABC üç basamaklı, AB ve BC iki basamaklı sayılar olmak üzere, üç basamaklı ABC sayısı aşağıdaki gibi çözümlenebilir.
ABC = 10 . AB + C
= 100A + BC

Çözümlü Sorular 

BASAMAK KAVRAMI SORULARI VE ÇÖZÜMLERİ

Şenol Hoca: Sayı Basamakları

Hocalara Geldik: Sayı Basamakları 1

Hocalara Geldik: Sayı Basamakları 2

BİR YORUM YAZIN

ZİYARETÇİ YORUMLARI - 0 YORUM

Henüz yorum yapılmamış.

Basamak Kavramı Konu Anlatımı Örnekler Tyt Sayı Basamakları Çözümleme

Örnek: 
AB ve BA iki basamaklı sayılar olmak üzere,
AB - BA = 63
olduğuna göre, A . B çarpımı en çok kaçtır?
A) 12    B) 14    C) 16    D) 18    E) 21

Çözüm: AB = 10.A+B ve BA = 10.B+A dır.
AB - BA=(10.A + B) - (10.B + A)
63=10.A + B - 10.B - A
63=9.A - 9.B
63=9.(A - B)
A - B = 7 dir.
A . B çarpımının en çok olması için A = 9 ve B = 2 olmalı. Buna göre, A . B = 9 . 2 = 18 olur. Cevap D

Örnek: Bir birim uzunluğundaki çubuk kullanılarak doğal sayılar yazılacaktır. Bu sayılardaki rakamların biçim ve boyutları aşağıda verilen şekilde olacaktır. Her rakamı yazmak için kullanılan çubuk sayısı, o rakamın altında parantez içinde verilmiştir. En az sayıda çubuk kullanılarak yazılabilecek, rakamları birbirinden farklı dört basamaklı en küçük doğal sayının rakamları toplamı kaçtır?
A)11    B) 12    C) 13   D) 14    E) 15

Çözüm: Öncelikle bir örnekle verileni anlamaya çalışalım. 478 sayısını yazmak için kaç çubuk kullanmak gerekir?
478 sayısını yazmak için 4 + 3 + 7 = 14 çubuk kullanmak gerekir. Şimdi sorulan sorunun cevabını bulalım: En az sayıda çubuk kullanılacağına göre,
1 rakamı için 2 çubuk,
7 rakamı için 3 çubuk,
4 rakamı için 4 çubuk,
2, 3 ve 5 rakamı için 5 çubuk kullanmak gerekir.
Rakamları birbirinden farklı dört basamaklı en küçük sayıyı oluşturmak için 5 çubukla yazılabilecek sayılardan 2 yi kullanmak gerekir. Buna göre, 1, 7, 4 ve 2 rakamlarını kullanarak yazılabilecek dört basamaklı en küçük doğal sayı 1247 olup rakamları toplamı 1 + 2 + 4 + 7 = 14 tür. Cevap D

Örnek: NN iki basamaklı bir doğal sayı ve m bir pozitif tam sayı olmak üzere,
NN = 4.m + 3 eşitliğini sağlayan N rakamlarının toplamı kaçtır?
A) 12 B) 13 C) 14 D) 15 E) 16

Çözüm: NN iki basamaklı bir doğal sayı ve m pozitif tam sayı ise
NN = 10.N + N = 11.N dir.
11.N = 4 . m + 3
11 . N - 3 = 4 . m
N rakamının 11 katının 3 eksiği, 4 e tam bölünmelidir.
N=1 için,11.1-3=8=4.2
N=5 için, 11.5-3=52=4.13
N =9 için, 11 . 9 - 3 = 96 = 4.24 tür.
Buradan, N = 1, N = 5, N = 9 için eşitlik sağlanır. Buna göre, N rakamlarının toplamı 1 + 5 + 9 = 15 tir. Cevap D