Alt Küme 9. Sınıf


Alt Kümenin Özellikleri


Alt Küme Sayısı
n elemanlı bir kümenin alt küme sayısı 2 üzeri n’dir.
n elemanlı bir kümenin, kendisi hariç alt kümelerinin (özalt kümelerinin) sayısı 2 üzeri n eksi 1’dir.
Boş kümenin alt küme sayısı 2 üzeri 0 = 1’dir.
Yani boş kümenin alt kümesi yalnızca kendisidir.
a ve b, A kümesinin elemanları olsun.
A kümesinin alt kümelerinde:
- a ve b’den yalnız biri bulunur ifadesi:
- a’nın bulunup, b’nin bulunmadığı,
- b’nin bulunup, a’nın bulunmadığı
durumlarını kapsar. Bu ifade, “a ya da b bulunur” şeklinde de ifade edilebilir.
- a veya b bulunur ifadesi:
- a’nın bulunup, b’nin bulunmadığı,
- b’nin bulunup, a’nın bulunmadığı,
- a ve b’nin birlikte bulunduğu
durumlarını açıklar.
Alt küme Çözümlü Örnekler
Kümeler Online Testler Tıklayın
Şenol Hoca Alt Kümeler konu anlatımı videosu
Halil İbrahim Tasova – Alt küme konu anlatımı videosu
Çözümlü Test Soruları
Soru 1:
A = {1, 2, 3} kümesinin alt kümelerinin kaç tanesinde 2 elemanı bulunur?
A) 2
B) 3
C) 4
D) 5
E) 6
Çözüm:
- 2 elemanını sabit tutup diğer elemanları (1 ve 3) seçmeye göre alt kümeler oluşturulur.
- 2’nin bulunduğu alt kümeler: {2}, {1,2}, {2,3}, {1,2,3} → 4 tane.
Cevap: C
Soru 2:
B = {a, b, c, d} kümesinin 3 elemanlı kaç alt kümesi vardır?
A) 3
B) 4
C) 6
D) 8
E) 12
Çözüm:
- Kombinasyon formülüyle: C(4,3) = 4.
- Alt kümeler: {a,b,c}, {a,b,d}, {a,c,d}, {b,c,d}.
Cevap: B
Soru 3:
C = {x, y, z} kümesinin öz alt küme sayısı kaçtır?
A) 5
B) 6
C) 7
D) 8
E) 9
Çözüm:
- Toplam alt küme sayısı: 2³ = 8.
- Öz alt küme sayısı: 8 – 1 = 7 (kendisi hariç).
Cevap: C
Soru 4:
D = {1, 2, 3, 4, 5} kümesinin alt kümelerinin kaç tanesinde 3 veya 5 bulunur?
A) 16
B) 20
C) 24
D) 28
E) 32
Çözüm:
- Tüm alt kümeler: 2⁵ = 32.
- 3 ve 5’in olmadığı alt kümeler: {1,2,4} → 2³ = 8.
- En az biri bulunanlar: 32 – 8 = 24.
Cevap: C
Soru 5:
E = {a, b, c} kümesinin alt kümelerinin kaç tanesinde a bulunur, b bulunmaz?
A) 1
B) 2
C) 3
D) 4
E) 5
Çözüm:
- a sabit, b yok, c isteğe bağlı.
- İstenen alt kümeler: {a}, {a,c} → 2 tane.
Cevap: B
Soru 6:
F = {1, 2, 3, 4} kümesinin alt kümelerinin kaç tanesinde 1 ve 2 birlikte bulunur?
A) 2
B) 3
C) 4
D) 5
E) 6
Çözüm:
-
1 ve 2 sabit, diğer elemanlar (3,4) isteğe bağlı.
-
Alt kümeler: {1,2}, {1,2,3}, {1,2,4}, {1,2,3,4} → 4 tane.
Cevap: C
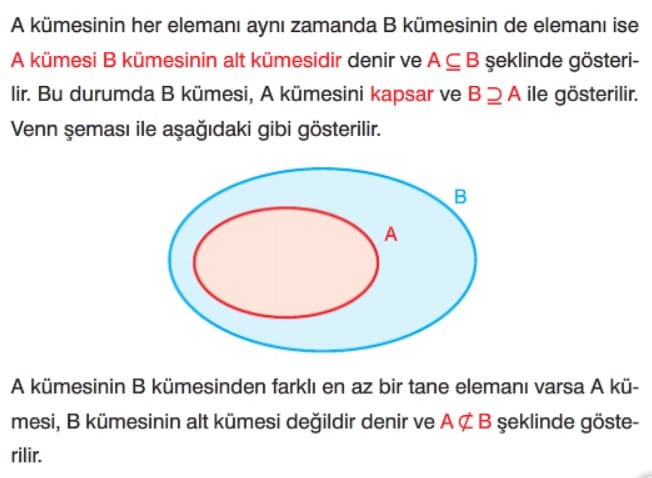
Alt kümelerin özellikleri: Her küme kendisinin de alt kümesidir. Boş küme tüm kümelerin alt kümesidir. A kümesi ve B kümesi birbirinin alt kümeleri ise bu iki küme eşit kümelerdir. B kümesinin A kümesinin alt kümesi olduğunu gösterip venn şeması ile gösterelim. B kümesinin her elemanı aynı zamanda A kümesinin de elemanı olduğu için B kümesi A kümesinin alt kümesidir.
A ve B iki küme olsun. A kümesinin tüm elemanları aynı zamanda B kümesinin de elemanı ise o zaman A kümesi B kümesinin alt kümesidir denir ve A⊂B şeklinde gösterilir. Bir kümenin kendisinden başka tüm alt kümelerine öz alt küme denir. n elemanlı bir kümenin tüm alt kümelerinin sayısı 2n formülü ile bulunur. Öz alt küme sayısı ise alt küme sayısının 1 eksiğidir yani 2n – 1 formülü ile hesaplanır. Örneğin, A kümesi A = {a, b, c, d, e} elemanlarından oluşan 5 elemanlı bir küme ise A kümesinin alt küme sayısı 2 üzeri 5′ den 32, özalt küme sayısı ise 1 eksiği yani 31’dir.
Soru: A = { x: x küçük eşit 5, x doğal sayıdır } kümesinin alt kümelerinin kaç tanesinde;
a. 0 bulunmaz?
b. 0 bulunur?
c. 1 ve 2 bulunur?
d. 1 veya 2 bulunur?
Çözüm: (x küçük eşit 5, x doğal sayı) ise x in alabileceği değerler; 0, 1, 2, 3, 4 ve 5 tir. Bu durumda, A = {0, 1, 2, 3, 4, 5} olur.
a. A kümesinden 0 sayısını çıkarırsak geriye 5 tane eleman kalır. Bu 5 tane eleman ile içinde 0 sayısı bulunmayan 25 = 32 tane alt küme yazılabilir.
b. A kümesindeki 0 sayısı hariç geri kalan 5 eleman ile 25 = 32 tane alt küme yazılabilir. Bu alt kümelerin her birine 0 sayısını eklersek A kümesinin 32 alt kümesinde 0 bulunmuş olur.
c. A kümesindeki 1 ve 2 sayısı hariç geriye kalan 4 tane eleman ile 24 =16 tane alt küme yazılabilir. Bu alt kümelerin her birine hem 1 hem de 2 sayısını eklersek A kümesinin 16 alt kümesinde 1 ve 2 sayısı bulunmuş olur.
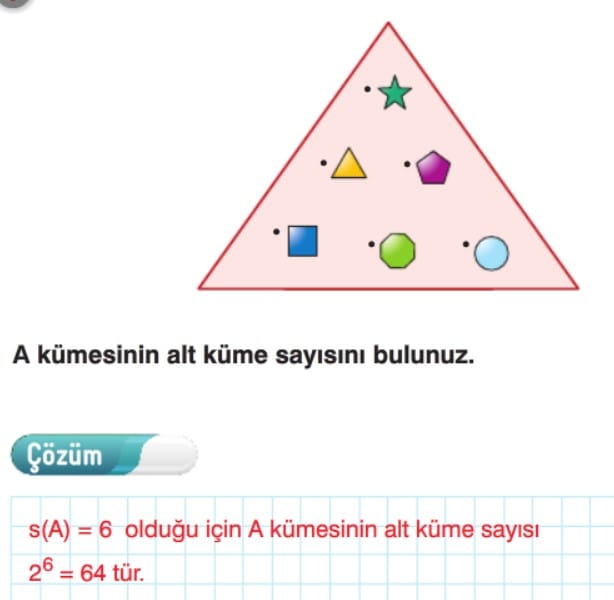
d. s(A) = 6 olduğundan A kümesinin alt kümelerinin sayısı 26 = 64 tür. A kümesindeki 1 ve 2 sayısı hariç geriye kalan 4 tane eleman ile 24 = 16 tane alt küme yazılabilir. A kümesinin tüm alt kümelerinin sayısından, içinde 1 ve 2 sayısı olmayan alt kümelerinin sayısını çıkardığımızda; içinde 1 veya 2 bulunan alt küme sayısını bulmuş oluruz. Buna göre, A kümesinin 64 – 16 = 48 alt kümesinde 1 veya 2 bulunur.
Alt Küme Nedir? Bir kümenin, elemanlarının herhangi bir sırayla sıralanmamış hallerine alt küme denir. Örneğin, {1, 2} kümesinin alt kümeleri {1}, {2} ve {1, 2}’dir.
Alt Küme Sayısı Formülü: Bir kümenin n elemanlı olduğunu düşünelim. O zaman bu kümenin alt küme sayısı 2^n’dir. Bu formül, bir elemanın bir alt küme içinde bulunup bulunmamasını düşünerek açıklanabilir. Her eleman için iki seçenek vardır: alt kümede bulunur veya bulunmaz. Dolayısıyla, n elemanlı bir kümenin alt küme sayısı 2^n olur.
Örnek: {a, b, c} kümesinin alt kümeleri: {}, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} toplamda 2^3 = 8 adettir.
Permütasyon ve Kombinasyon ile İlişki: Permütasyon ve kombinasyon kavramları da alt küme sayısıyla ilgilidir. Permütasyonlar, bir kümedeki elemanların sıralanış şekillerini ifade ederken, kombinasyonlar ise sıralama olmaksızın seçim yapmayı ifade eder. Alt küme sayısı, kombinasyonlara benzer bir prensiple hesaplanabilir.
Alt küme sayısı formülü, kombinasyon formülü C(n, k) ile de ifade edilebilir. n elemanlı bir kümeden k eleman seçme şeklindeki kombinasyon sayısı C(n, k) şu şekilde hesaplanır:
Bu formülde
n faktöriyelini ifade eder.
Soru: Bir zarın atılması durumunda ortaya çıkabilecek alt kümelerin sayısı kaçtır?
Çözüm: Bir zar atıldığında ortaya çıkabilecek alt kümeler, zarın üst yüzlerinin kombinasyonlarına denk gelir. Zarın 6 yüzü olduğu için toplam alt küme sayısı
26‘dır. 26= 64
Bu nedenle, bir zarın atılması durumunda ortaya çıkabilecek alt kümelerin sayısı 64’tür.

















Çok bilgi edindim sağolun😀
güzel bilgiler edindim
Gerçekten verdiğiniz bilgiler bana çok şey kazandırdı