Bu yazımızda Her ve Bazı Niceleyicileri konu anlatımı yer almaktadır. Konu anlatımını bitirdikten sonra Açık Önermeler ve Niceleyiciler Çözümlü Sorular yazımıza da bakabilirsiniz.
Sonraki Konu: Tanım, Aksiyom, Teorem ve İspat Kavramları

Açık Önermeler

Çözümlü Sorular

Niceleyiciler

Çözümlü Sorular

Çözümlü Örnek Test Soruları: Açık Önermeler – Her ve Bazı Niceleyicileri

Soru 1
p(x): “x bir asal sayıdır.” açık önermesi için, “Bazı x değerleri asal sayıdır.” ifadesi matematiksel olarak nasıl ifade edilir?
A) Her x asal sayıdır.
B) En az bir x asal sayıdır.
C) Hiçbir x asal sayı değildir.
D) Tüm x asal sayı değildir.

Çözüm
“En az bir x asal sayıdır” ifadesi matematiksel olarak “var x p(x)” şeklinde ifade edilir. Bu, açıkça bazı x değerlerinin asal sayı olduğunu belirtir.
Doğru cevap: B

Soru 2
q(x): “x bir çift sayıdır.” açık önermesi için, “Tüm x değerleri çift sayıdır.” ifadesi doğru olabilir mi?
A) Evet, tüm x değerleri çifttir.
B) Hayır, çünkü bazı x değerleri tektir.
C) Hayır, çünkü çift sayılar yalnızca pozitif değerler alabilir.
D) Evet, yalnızca negatif x değerleri için geçerlidir.

Çözüm
“Tüm x değerleri çift sayıdır” ifadesi doğru olamaz çünkü tam sayıların bir kısmı tektir.
Doğru cevap: B

Soru 3
Bir açık önerme r(x): “x bir doğal sayıdır ve x > 0’dır.” ifadesi için, “Tüm x değerleri pozitiftir.” ifadesi matematiksel olarak nasıl yazılır?
A) var x r(x)
B) her x r(x)
C) hiçbir x r(x)
D) tüm x r(x) değildir

Çözüm
“Tüm x değerleri pozitiftir” ifadesi matematiksel olarak “her x r(x)” şeklinde yazılır.
Doğru cevap: B

Soru 4
Bir açık önerme p(x): “x² > x” ifadesi için, x = 2 değeri sağlıyor mu?
A) Evet
B) Hayır
C) Bazen
D) Kesin değil

Çözüm
x = 2 için, x² > x ifadesi şöyle hesaplanır:
2² > 2 → 4 > 2. Bu ifade doğrudur.
Doğru cevap: A

Soru 5
Bir açık önerme t(x): “x bir tam sayıdır ve negatif bir sayıdır.” ifadesi için, “En az bir x negatif bir tam sayıdır.” ifadesi matematiksel olarak nasıl yazılır?
A) var x t(x)
B) her x t(x)
C) hiçbir x t(x)
D) tüm x t(x) değildir

Çözüm
“En az bir x negatif bir tam sayıdır” ifadesi matematiksel olarak “var x t(x)” şeklinde yazılır.
Doğru cevap: A

Soru 6
Bir açık önerme q(x): “x bir tam sayı ve çift bir sayıdır.” için, tüm tam sayıların çift olduğunu ifade eden önerme doğru mudur?
A) Evet, tüm tam sayılar çifttir.
B) Hayır, bazı tam sayılar tektir.
C) Hayır, çünkü çift sayılar sadece pozitif değerler alabilir.
D) Evet, sadece negatif tam sayılar için geçerlidir.

Çözüm
Tüm tam sayılar çift değildir; bazıları tektir. Bu nedenle “Tüm tam sayılar çifttir” ifadesi doğru olamaz.
Doğru cevap: B

Mantıkta, bir önermenin doğruluk değeri, o önermenin ele aldığı nesnenin (veya nesnelerin) durumuna bağlı olan önermeye açık önerme denir. Örneğin, “Bugün hava güneşli” önermesi, “Bu kitap kırmızı” önermesi, “2+2=4” önermesi açık önermelerdir.

Önüne geldiği elemanın çokluğunu (niceliğini) belirten bazı, her sözcüklerine niceleyiciler denir. Bazı niceleyicisi, en az bir tane anlamına gelir. Bu niceleyici yukarıdaki şekilde verildiği gibi gösterilir. Bazı x, p(x) ifadesi “en az bir x için p(x)” diye okunur. Her niceleyicisi bütün niceleyicisi ile aynı anlamı taşır. Bu niceleyici yukarıda şekilde verilidiği gibi gösterilir. Her x p(x) ifadesi “her x için p(x)” diye okunur. “Bazı x, p(x)” önermesinin doğru olduğunu göstermek için, p(x) in doğru olduğunu gösteren örnek yeterlidir. Her x p(x) önermesinin yanlış olduğunu göstermek için, p(x) i yanlış olduğunu gösteren bir örnek yeterlidir.

Örnek: Sembolik mantık kullanılarak verilen, “bazı x tam sayıları, x – 5 küçük eşittir 7” ifadesini sözel olarak ifade edelim.
Çözüm: “Bazı tam sayıların 5 eksiği 7 ye eşit veya 7 den küçüktür.” veya “En az bir tam sayının 5 eksiği 7 den küçük eşittir.” şeklinde ifade edilir.

Örnek: “Bazı gerçek sayıların 50 fazlası 100 den büyüktür.” önermesini sembolik mantık olarak ifade edelim.
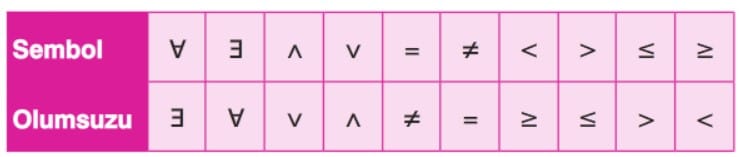
Çözüm: “Bazı gerçek sayıların 50 fazlası 100 den büyüktür.” önermesinin sembolik ifadesi “bazı x eleman gerçek sayı için, x + 50 büyüktür 100” olur. Bazı niceleyicisinin olumsuzu her niceleyicisi, her niceleyicisinin olumsuzu bazı niceleyicisidir.

Örnek: “Bazı tam sayılar negatiftir.” önermesinin olumsuzu “Her tam sayı negatif değildir.” önermesidir.
Örnek: “Her gün güneş doğar.” önermesinin olumsuzu, “Bazı günler güneş doğmaz.” cümlesidir.

• Her ve Bazı Niceleyicilerinin Karşılaştırılması
• “Her” ve “bazı” niceleyicileri arasında önemli bir fark vardır. “Her” niceleyicisi, bir önermede yer alan nesnenin veya nesnelerin hepsini kapsarken, “bazı” niceleyicisi bu nesnelerin bir kısmını kapsar.
• Örneğin, “Her insan ölümlüdür” önermesi doğrudur çünkü insan olan tüm şeyler ölümlüdür. Ancak, “Bazı insanlar ölümlüdür” önermesi de doğrudur çünkü insan olan bazı şeyler ölümlüdür.
• Her ve Bazı Niceleyicilerinin Kullanımı
• Her ve bazı niceleyicileri, açık önermeleri daha spesifik hale getirmek için kullanılabilir. Örneğin, “Bugün hava güneşli” önermesi, “Her gün hava güneşli” önermesine göre daha az spesifiktir. Çünkü ikinci önerme, tüm günleri kapsarken, ilk önerme sadece bugünü kapsar.