Üçgende Açı ve Kenar İlişkileri Test Çöz 9. Sınıf Matematik (Üçgen Eşitsizliği)
Üçgenler, geometri konusunun temel taşlarından biridir ve açı ölçüleri ile kenar uzunlukları arasındaki ilişki, üçgenlerle ilgili problemlerin çözümünde kritik bir öneme sahiptir. Üçgen eşitsizliği, bir üçgenin kenar uzunlukları ile ilgili temel bir kuraldır ve bu kural, herhangi bir üçgenin bir kenarının uzunluğunun diğer iki kenarın toplamından küçük, farkından büyük olması gerektiğini belirtir. Ayrıca, büyük açının karşısında büyük kenarın, küçük açının karşısında ise küçük kenarın bulunduğu gerçeği, üçgenin açı ve kenar ilişkilerini anlamada önemli bir yer tutar. Yeni nesil testler, günlük hayatla ilişkilendirilmiş hikayeleri kullanarak, öğrencilerin bu kuralları hem pratik hem de teorik olarak kavramalarını sağlamayı hedefler.
9. Sınıf Üçgende Açı ve Kenar İlişkileri Konu Anlatımı
9. Sınıf Üçgenin Açı Ölçüleri ve Kenar Uzunlukları Arasındaki İlişki – Üçgen Eşitsizliği Testleri (Yeni Müfredat)
9. Sınıf Üçgende Açı ve Kenar İlişkileri Test 1 Çöz
9. Sınıf Üçgende Açı ve Kenar İlişkileri Test 2 Çöz
9. Sınıf Üçgende Açı ve Kenar İlişkileri Test 3 Çöz
9. Sınıf Üçgende Açı ve Kenar İlişkileri Test 4 Çöz
9. Sınıf Üçgende Açı ve Kenar İlişkileri Test 5 Çöz
9. Sınıf Üçgende Açı ve Kenar İlişkileri Test 6 Çöz
9. Sınıf Üçgende Açı ve Kenar İlişkileri Test 7 Çöz
9. Sınıf Üçgende Açı ve Kenar İlişkileri Test 8 Çöz
9. Sınıf Üçgende Açı ve Kenar İlişkileri Test 9 Çöz
Açı Kenar Bağıntıları ve Üçgen Eşitsizliği Çözümlü Sorular
Çözümlü Örnek Test Soruları: Açı Kenar Bağıntıları ve Üçgen Eşitsizliği
Soru 1:
Bir üçgende kenar uzunlukları sırasıyla a = 7, b = 10 ve c olarak verilmiştir. Bu üçgenin oluşabilmesi için c kenarının alabileceği değer aralığı nedir?
A) 3 < c < 17
B) 4 < c < 18
C) 5 < c < 16
D) 2 < c < 15
Cevap: A
Çözüm: Üçgen eşitsizliğine göre bir üçgenin oluşabilmesi için iki kenarın toplamı diğer kenardan büyük, farkı ise diğer kenardan küçük olmalıdır.
- a + b > c → 7 + 10 > c → c < 17
- b + c > a → 10 + c > 7 → c > 3
- a + c > b → 7 + c > 10 → Bu eşitsizlik zaten c > 3 ile sağlanmıştır.
Bu durumda 3 < c < 17 olur.
Soru 2:
Bir üçgende A, B, ve C açılarına karşılık gelen a, b, ve c kenarları sırasıyla a = 6, b = 8, c = 10 verilmiştir. Üçgende en büyük açı hangisidir?
A) A açısı
B) B açısı
C) C açısı
D) Hepsi eşit
Cevap: C
Çözüm: Üçgende en büyük açı her zaman en uzun kenarın karşısındaki açıdır. Burada en uzun kenar c = 10 olduğu için en büyük açı C açısıdır.
Soru 3:
Bir üçgende açı ölçüleri A açısı = 40 derece ve B açısı = 60 derece verilmiştir. Buna göre en uzun kenar hangisinin karşısındadır?
A) A açısının
B) B açısının
C) C açısının
D) Belirlenemez
Cevap: C
Çözüm: Üçgende en uzun kenar her zaman en büyük açının karşısındadır. Burada C açısı = 180 – 40 – 60 = 80 derece olduğu için en uzun kenar C açısının karşısındadır.
Soru 4:
Bir üçgende kenar uzunlukları x = 6, y = 8 ve z = 10 verilmiştir. Bu üçgenin dik üçgen olup olmadığını kontrol ediniz.
A) Dik üçgen
B) Dar açılı üçgen
C) Geniş açılı üçgen
D) Üçgen değildir
Cevap: A
Çözüm: Dik üçgen kontrolü için Pisagor Teoremi uygulanır:
z² = x² + y²
10² = 6² + 8² → 100 = 36 + 64 → 100 = 100.
Bu nedenle üçgen bir dik üçgendir.
Soru 5:
Bir üçgende x + y = 12, x – y = 4 ise x ve y değerleri nelerdir?
A) x = 8, y = 4
B) x = 6, y = 6
C) x = 10, y = 2
D) x = 7, y = 5
Cevap: A
Çözüm: İki denklem toplanır: (x + y) + (x – y) = 12 + 4 → 2x = 16 → x = 8.
x yerine konulursa x + y = 12 → 8 + y = 12 → y = 4.
Soru 6:
Bir üçgende kenar uzunlukları sırasıyla a = 5, b = 7 ve c = 10 olarak verilmiştir. Bu üçgenin dar açılı bir üçgen olup olmadığını kontrol ediniz.
A) Dar açılı üçgen
B) Dik üçgen
C) Geniş açılı üçgen
D) Üçgen değildir
Cevap: A
Çözüm: Kenarlar arasında c² < a² + b² ise üçgen dar açılıdır. Burada 10² < 5² + 7² → 100 < 25 + 49 → 100 < 74 değildir, bu nedenle üçgen dar açılıdır.
Soru 7:
Bir üçgenin kenarları a = 9, b = 12 ve c = 15 olarak verilmiştir. Üçgenin en büyük açısını bulunuz.
A) 90 derece
B) 60 derece
C) 120 derece
D) 45 derece
Cevap: A
Çözüm: En büyük açıyı bulmak için kosinüs teoremi uygulanır:
cos(C) = (a² + b² – c²) / (2 * a * b)
cos(C) = (9² + 12² – 15²) / (2 * 9 * 12)
cos(C) = (81 + 144 – 225) / 216 → cos(C) = 0 → C = 90 derece.
Soru 8:
Bir üçgende kenarlar sırasıyla 3, 4 ve 5 cm ise bu üçgenin çevresi kaç santimetredir?
A) 9
B) 10
C) 11
D) 12
Cevap: D
Çözüm: Üçgenin çevresi tüm kenarların toplamıdır: 3 + 4 + 5 = 12 santimetre.
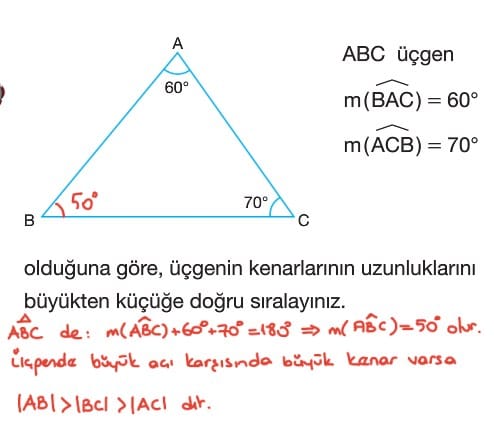
Soru: İç açıları 60 derece ve 70 derece olan bir ABC üçgeninin kenar uzunluklarını küçükten büyüğe doğru sıralayınız.
Çözüm: ABC üçgeninde iç açıların ölçüleri toplamı yüz seksen derece olacağından diğer açının ölçüsü elli derece olarak bulunur. Dolayısıyla elli derecenin karşısındaki kenar en küçük kenar, sonrasında ise altmış derecenin karşısındaki kenar ve son olarak da 70 derecenin karşısındaki kenar gelir.
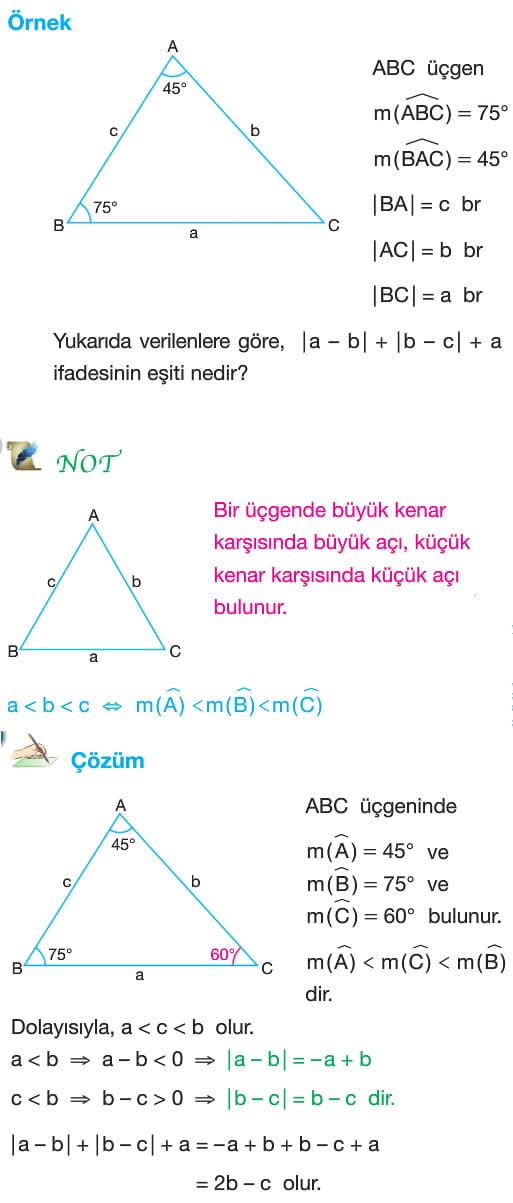
Soru: Bir ABC üçgeninde A açısının ölçüsü kırk beş derece, B açısının ölçüsü yetmiş beş derecedir. Verilen bilgilere göre |a – b| + |b – c| + a ifadesinin eşitini bulunuz. Not: Bir üçgende büyük açının karşısında büyük kenar bulunur.
Çözüm: ABC üçgeninde 45 + 75 + C = 180 olacağından C açısının ölçüsü 60 derece olarak bulunur. Buradan b > c > a eşitsizliği elde edilir. a b den küçük olduğu için |a – b| işleminin sonucu b – a, b c den büyük olduğu için |b – c| işleminin sonucu b – c olarak bulunur. Dolayısıyla |a – b| + |b – c| + a = b – a + b – c + a = 2b – c olur.
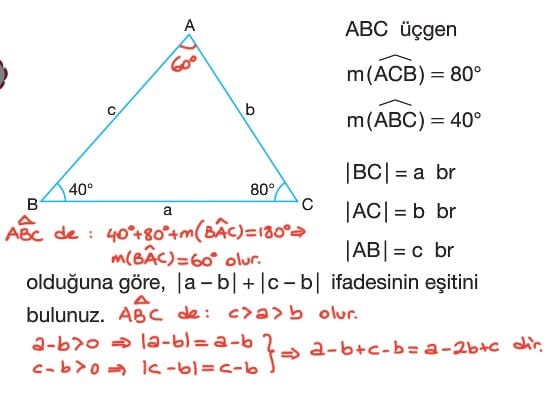
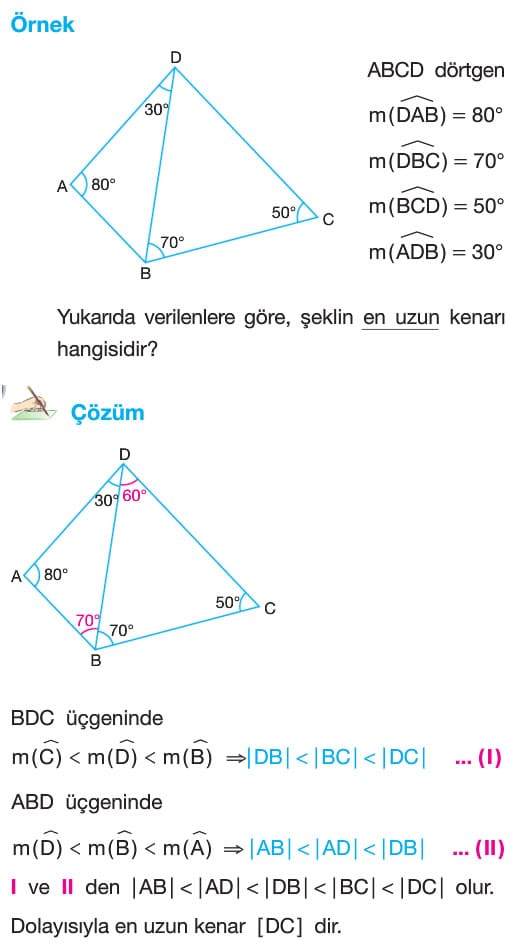
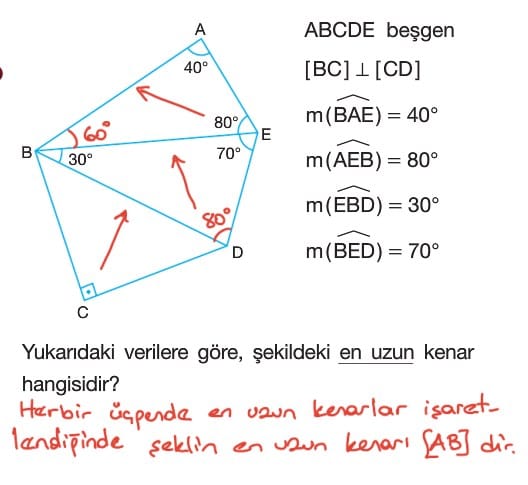
Soru: BD kenarı ortak olan ABD ve BDC üçgenleri veriliyor. BAD açısının ölçüsü seksen derece, ADB açısının ölçüsü otuz derece, DBC açısının ölçüsü yetmiş derece ve BCD açısının ölçüsü elli derece olarak veriliyor. Buna göre verilen şekilde en uzun kenar hangisidir?
Çözüm: BDC üçgeninde iç açıların ölçüleri toplamından BDC açısının ölçüsü altmış derece olarak bulunur. Dolayısıyla BDC üçgeninin en uzun kenarı DC uzunluğudur. ABD üçgeninde iç açıların toplamından ABD açısının ölçüsü yetmiş derece olarak bulunur. Dolayısıyla ABD üçgeninde en uzun kenar BD uzunluğudur. BDC üçgeninde kenar uzunlukları arasındaki bağıntı BD < BC < DC olduğundan verilen şekilde en uzun kenar DC kenarıdır.

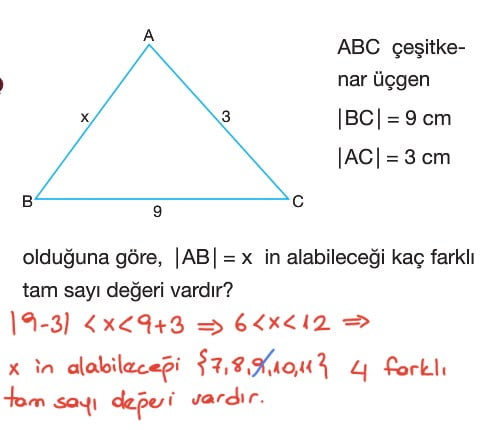
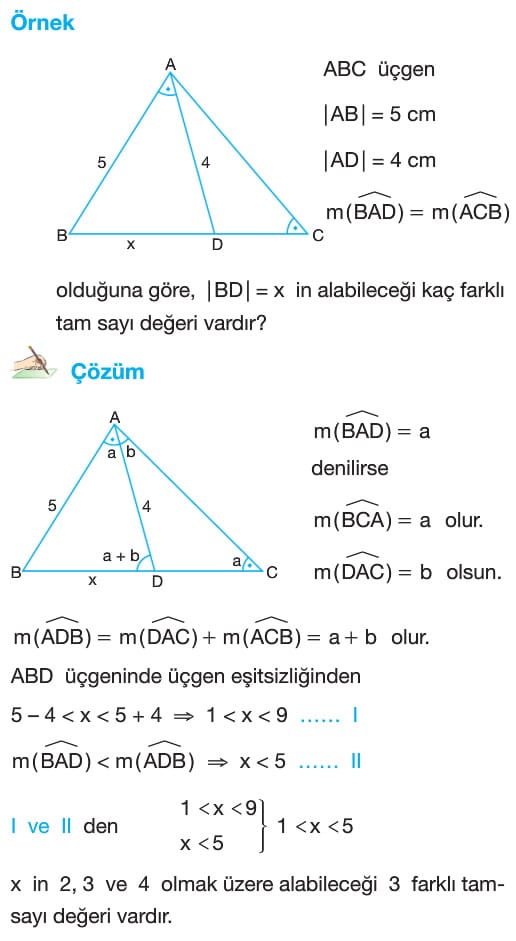
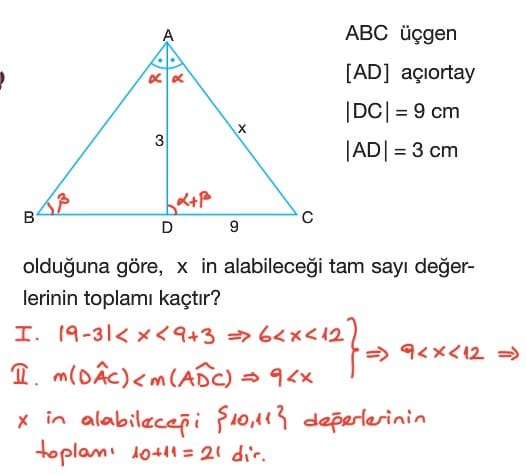
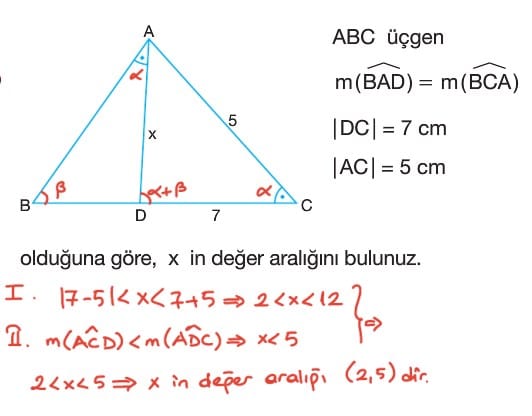







aynen c doğru katılıyorum
ilk soru yanlış c şıkkı doğru